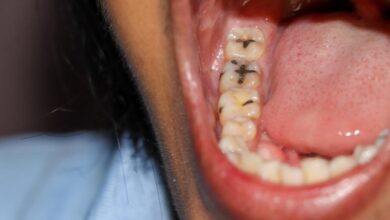
Kakeya dohad, desetiletý matematický problém, je vyřešen ve třech rozměrech

Matematici řeší desetiletí starou rotující jehlu
Dlouhá dohad Kakeya, která zahrnuje otáčení nekonečně úzké jehly, udržovala matematiky hádání – až dosud
Sean Gladwell/Getty Images
Je vzácné číst o „velkolepý pokrok“Nebo„jednou za století„Výsledkem je matematika. To je z dobrého důvodu: pokud problém neměl řešení po mnoho let, pak k jejímu řešení je obvykle zapotřebí zcela nové přístupy a nápady.
Od roku 1917 se od roku 1917 staví odborníci nad souvisejícími problémy. Ale v předtiskovém článku zveřejněném v únoru, matematik Hong Wang z New York University a její kolega Joshua Zahl z University of British Columbia konečně konečně prokázáno Trojrozměrná verze dohadu Kakeya. „Je to jeden z nejlepších matematických úspěchů 21. století,“ řekl matematik Eyal Lubetzky z N.Y.U. v a nedávné Tisková zpráva.
Předpokládejme, že na stole je nekonečně úzká jehla. Nyní ji chcete otočit o 360 stupňů tak, aby špička jehly ukazovala jednou v každém směru roviny. Chcete -li to provést, můžete držet jehlu uprostřed a otáčet ji. Jak se to otáčí, jehla poté zakrývá povrch kruhu.
O podpoře vědecké žurnalistiky
Pokud se vám tento článek líbí, zvažte podporu naší oceněné žurnalistiky předplatné. Zakoupením předplatného pomáháte zajistit budoucnost působivých příběhů o objevech a myšlenkách, které dnes formují náš svět.
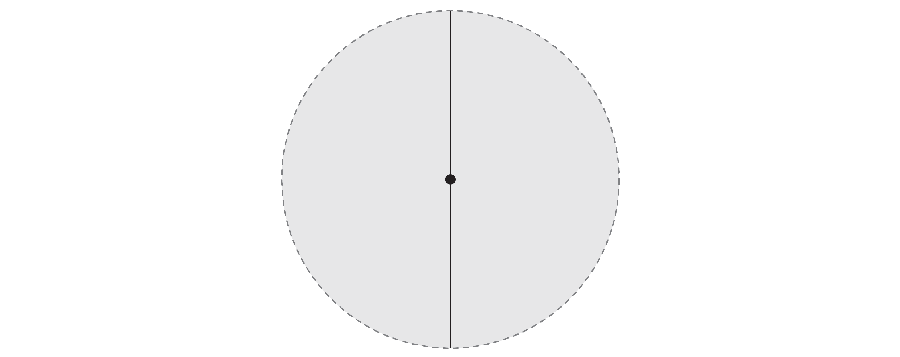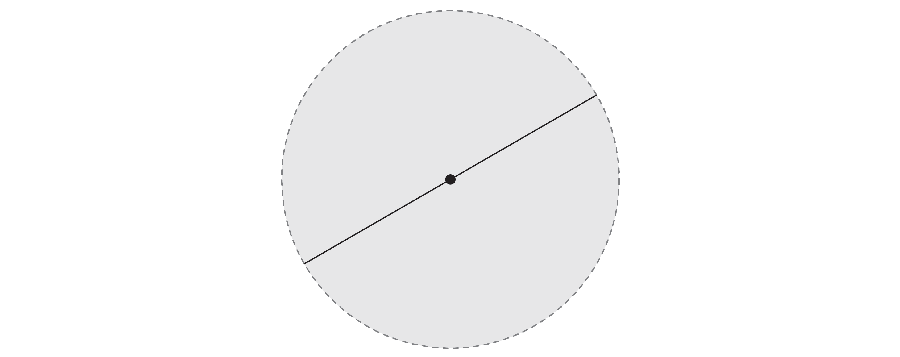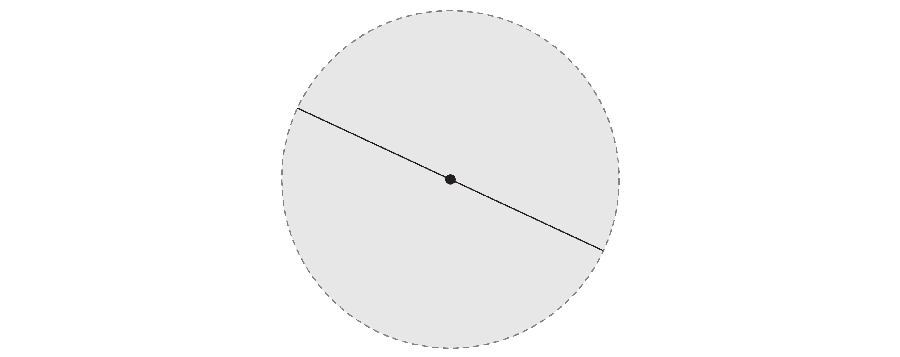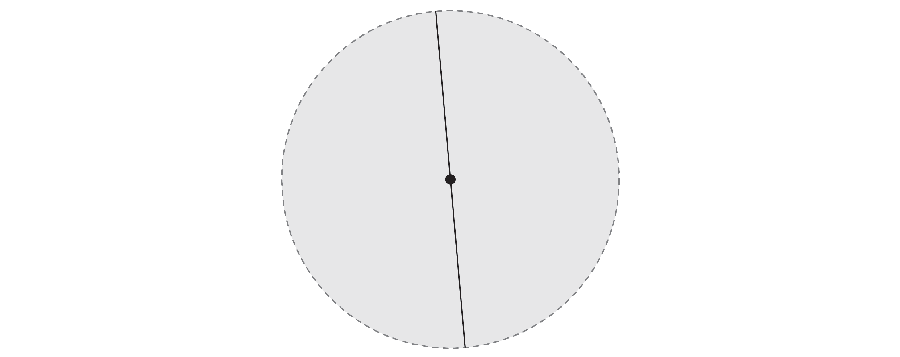
Ale pokud jste chytří, jehla může udělat svou 360 stupňovou cestu a zároveň si vzít méně místa. V roce 1917 chtěl matematik Sōichi Kakeya prozkoumat nejmenší oblast potřebnou k otáčení jehly. Například otáčením nejen vnějšího konce jehly, ale také její střed, můžete získat oblast, která odpovídá trojúhelníku se zakřivenými stranami.
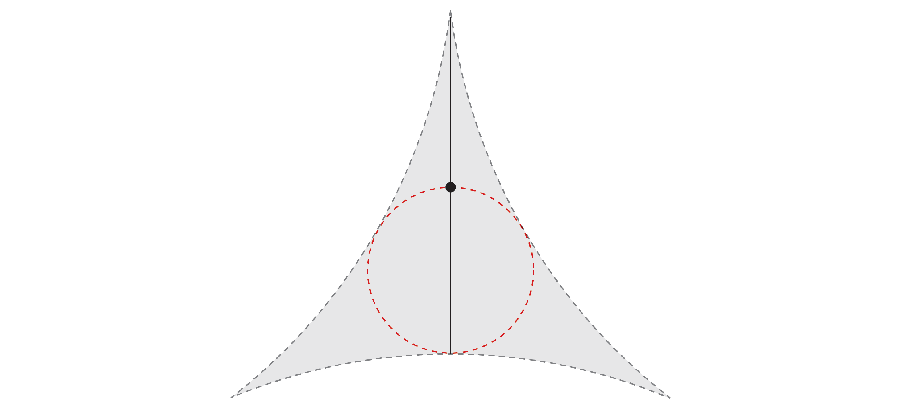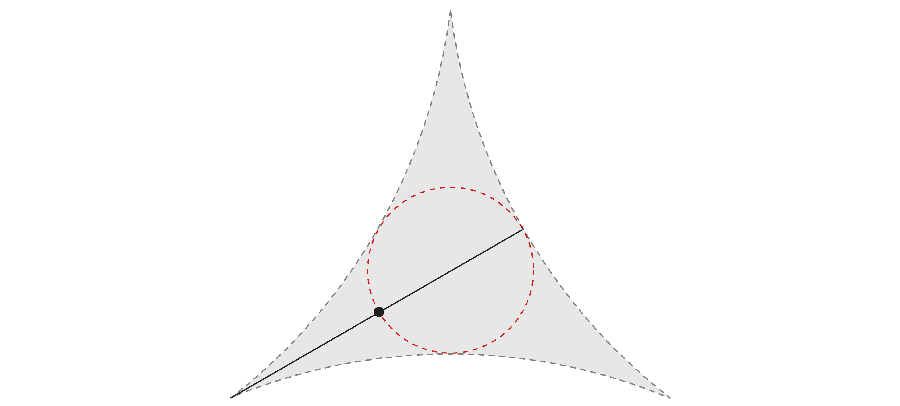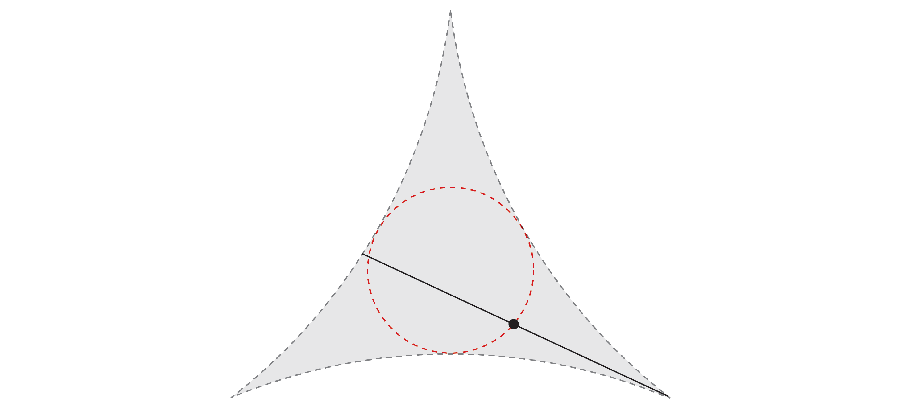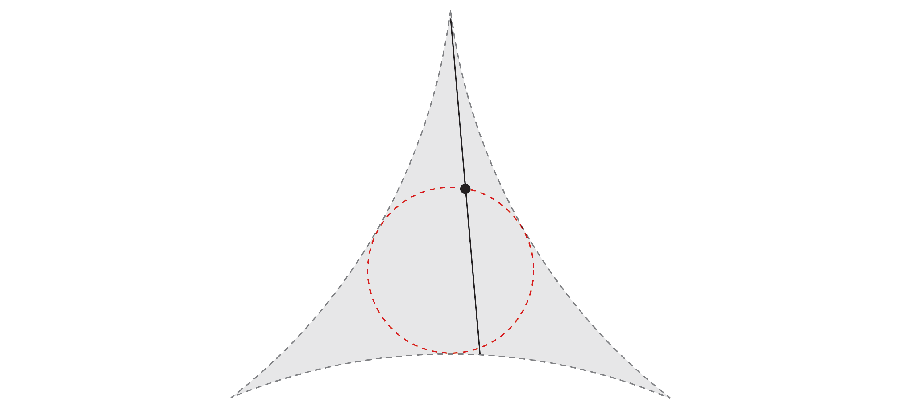
O několik let později, Matematik Abram Besicovitch Udělal nečekaný objev. Pokud stále pohybujete jehlou tam a zpět jako komplexní paralelní parkovací manévr, povrch, který nekonečně úzké kryty jehly mohou mít ve skutečnosti celkovou plochu nuly.
Rozměr oblasti nulové?
Odtud se odborníci začali ptát, jakou dimenzi má tento „povrch Kakeya“. Obvykle jsou povrchy v rovině, jako je obdélník nebo kruh, dvourozměrné. Existují však výjimky: Například fraktály mohou mít také zlomkové rozměry, což znamená, že mohou být například 1,5-dimenzionální.
Protože povrchy Kakeya mohou vypadat velmi zubaté, otázka dimenze je zřejmá. Ve skutečnosti má důsledky pro mnoho dalších oblastí matematiky, včetně harmonické analýzy, která rozděluje komplikované matematické křivky na součty jednodušších funkcí a teorie geometrické míry.
Ve skutečnosti byl v roce 1971 matematik Roy Davies schopen prokázat že povrch Kakeya je vždy dvourozměrný, i když jeho oblast zmizí. Ale v matematice se lidé zajímají o obecné výsledky. Odborníci chtěli problém vyřešit n Rozměry – jehla, která se otočí podél všech n Prostorové pokyny vždy pokrývají n-Dmenzionální objem? Tato hypotéza je nyní známá jako dohad Kakeya.
Trojrozměrný případ se ukázal jako extrémně tvrdý ořech. V průběhu desetiletí byli odborníci schopni vyloučit možnost, že rotující jehla pokrývá objem s méně než 2,5 prostorovými rozměry, ale to bylo tak daleko, jak se dostali.
Wang a Zahl však nebyli odrazováni a krok za krokem propracovali. Díky pečlivému úsilí se jim postupně podařilo eliminovat všechny případy, ve kterých by krytý objem měl rozměr menší než tři.
Tímto způsobem byli nakonec schopni prokázat dohad Kakeya ve třech prostorových rozměrech, což ukazuje, že objem pokrytý jehlou je vždy trojrozměrný. V nedávné tiskové zprávě matematik Guido de Philippis z NYU poznamenal: „Očekávám, že jejich myšlenky povedou k řadě vzrušujících průlomů v nadcházejících letech.“
Tento článek se původně objevil v Spektrum vědy a byl reprodukován se svolením.