Studenti najdou skrytou sekvenci Fibonacci v klasické puzzle pravděpodobnosti
Variace puzzle zvané „pick-up holesis problém“ se zeptá na následující otázku: Pokud mám nějaký počet tyčinek s náhodnými délkami mezi 0 a 1, jaké jsou šance, že žádné tři z těchto tyčinek nemohou tvořit trojúhelník? Ukázalo se, že odpověď na tuto quandary má neočekávanou paralelu se vzorem nalezeným napříč přírodou.
Fibonacci sekvence je uspořádaná sbírka čísel, ve kterých se každý termín rovná předchozích dvou sdaných dohromady. To je takto: 1, 1, 2, 3, 5, 8, 13, … a tak dále. Tato čísla se objevují prakticky všude. Pokud se podíváte na rostlinu se spirály, jako je borovicový kužel nebo ananas, s větší pravděpodobností než ne, počet spirál v každém směru bude po sobě jdoucí termíny sekvence Fibonacci. Ale pár mladých vědců byl překvapen, když zjistili, že tento vzorec a problém s pick-up jsou hluboce propojeny.
O podpoře vědecké žurnalistiky
Pokud se vám tento článek líbí, zvažte podporu naší oceněné žurnalistiky předplatné. Zakoupením předplatného pomáháte zajistit budoucnost působivých příběhů o objevech a myšlenkách, které dnes formují náš svět.
Problém s pick-up honíky je variantou problému „rozbité tyčinky“, který lze vysledovat zpět k nejméně 1854. Při jeho nejjednodušší iteraci se problém zlomené tyčinky ptá, že hůl náhodně na tři kusy může tvořit trojúhelník. (V problému s pick-up hůlky nemusí délky přidávat až do určitého celku, takže možné délky jsou distribuovány jinak.) O více než století později, v Říjen 1959 vydání z Vědecký Američan, Martin Gardner psal o problému se zlomenou hůlkou Pro svůj sloupec matematických her. Gardner to zdůraznil jako klasický příklad kontraintuitivní povaha problémů v pravděpodobnosti a statistice. V Papír předtišku Mladí vědci a jejich spolupracovníci, kteří zveřejnili na serveru arxiv.org, zkoumají novou variantu problému s pick-up.
Toto úsilí začalo, když Arthur Sun, první roční vysokoškolský student na University of Cambridge, vymyslel problém pro univerzitní matematickou soutěž. Jaká je pravděpodobnost, přemýšlel, že ze čtyř tyčinek s náhodnými délkami mezi 0 a 1 nemohl vytvořit trojúhelník? V době 12. srovnávače na Scotch College, střední škole v Austrálii, kde se on a Sun původně setkali, narušil pomoc svého přítele Edwarda Wanga. Společně Wang a Sun modelovali problém na svých počítačích a znovu a znovu probíhali náhodné pokusy, přičemž sledovali výsledky každé pokusy. Zdálo se, že pár se zdálo, že čtyři hole nemohly mezi nimi vyrobit trojúhelník velmi blízko jedné šesté době.
Brzy Wang a Sun začali přemýšlet, jaká byla odpověď pro větší seskupení tyčinek. Začlenili pomoc Davida Treebyho, matematika spojeného s australskou Monash University a učitelem na Scotch College. Skupina proběhla ještě více simulací a brzy se začal objevovat vzor.
Podle simulací vědců, pokud n byl počet tyčinek vybrán náhodně, šance, že mezi nimi nebude mít platný trojúhelník n Čísla Fibonacci se znásobila dohromady. Například, pokud si vyberete šest tyčinek náhodně, pravděpodobnost, že s nimi nemůžete vyrobit trojúhelník, je 1 / (1 × 1 × 3 × 5 × 8) = 1⁄240. Tým byl překvapen, že slavná sekvence byla spojena s problémem trojúhelníku. „Neměli bychom mít důvod mít podezření, že by to bylo,“ říká Treeby, „ale nebylo možné, aby to nebylo.“
Vědci začali vyvíjet důkaz toho, proč musí být toto spojení pravdivé, ale potřebovali odborníka na statistiku, aby to všechno spojil. Přinesli čtvrtého spolupracovníka, bývalého matematika Monasha Aidana Sudburyho. Když se k němu přiblížil tým, šťastně si užíval odchodu do důchodu.
„Okamžitě mě zasáhl, jaký to byl okouzlující problém,“ říká. „Skvělé!“ Společně čtyři vědci vypracovali solidní důkaz o vzoru, který si Sun a Wang všimli. Ačkoli Související výsledky Byly prokázány pomocí podobných metod a zahrnují širokou škálu problémů s tyčinkami a trojúhelníkem, někteří odborníci v terénu považují jednoduchost tohoto nového papíru osvěžující. „Co je na tom hezké, je to: Je to velmi dobře napsané,“ říká Steven Miller, matematik na Williams College a prezident Asociace Fibonacci. „Je to přístupné, je to snadné číst a rozšiřuje to velmi slavný problém.“
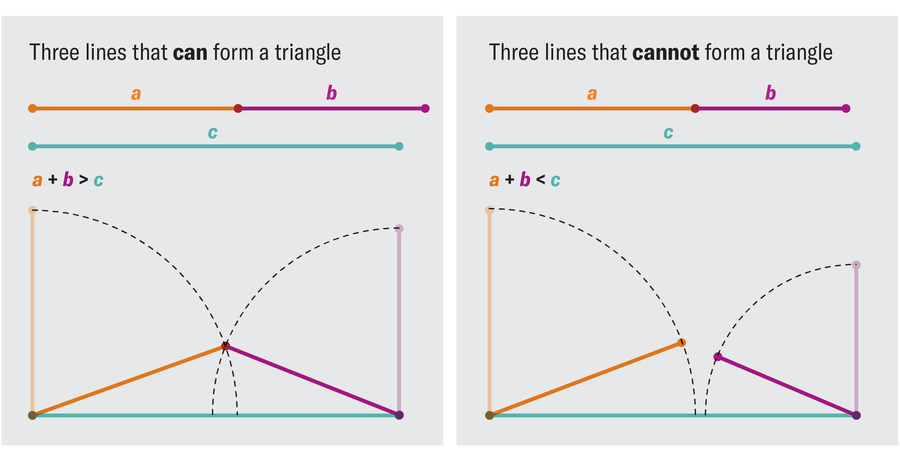
Chcete-li porozumět řešení vyzvednutí, přemýšlejte o nejmenším možném případu. Předpokládejme, že máte tři tyčinky s náhodnými velikostmi mezi 0 a 1.. Jakékoli tři tyčinky mohou tvořit trojúhelník, pokud, a pouze tehdy, pokud není žádná hůl delší než ostatní dva dohromady. Pokud máte tyčinky délek 1, 2 a 300, bez ohledu na to, jak široký je mezi nimi úhel, první dvě tyčinky se nikdy nemohly natáhnout dostatečně široké, aby se přizpůsobily třetí. Tomu se říká „nerovnost trojúhelníku“: pokud A, b a C představují délky tyčinek od nejkratších po nejdelší, nedokážou vytvořit jen trojúhelník, když A + b ≤ C.
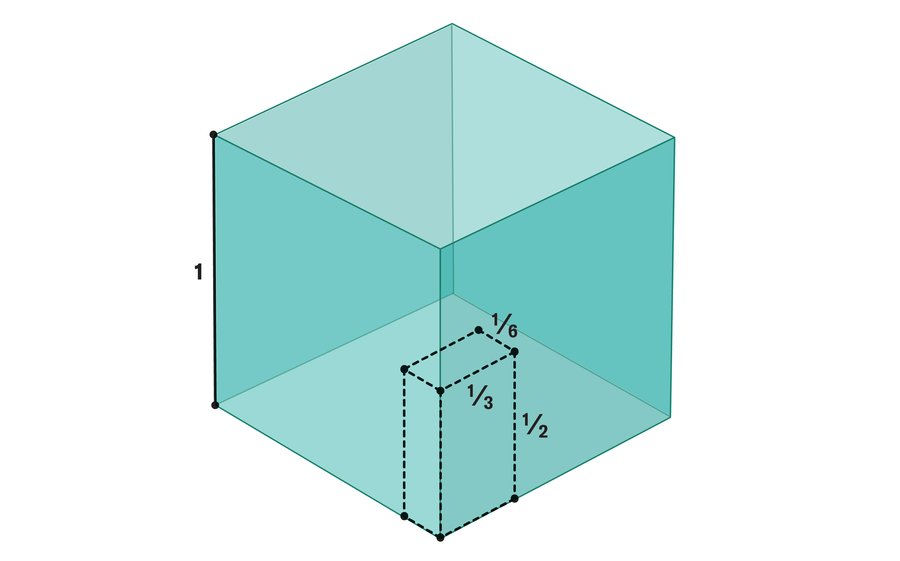
Pro nalezení pravděpodobnosti, že tři náhodné délky tvoří trojúhelník, mohou matematici považovat každou sadu tří délek za bod v trojrozměrném prostoru (například délky 1⁄2, 1⁄6 a 1⁄3 jsou zastoupeny bodem (1⁄2, 1⁄6,1⁄3)). Protože délky klesají mezi 0 a 1, může být sada všech takových bodů reprezentována jednotkou Cube:
Vědci se poté podívají na podmnožinu této krychle, kde body splňují nerovnost trojúhelníku – tvar, který vypadá takto:
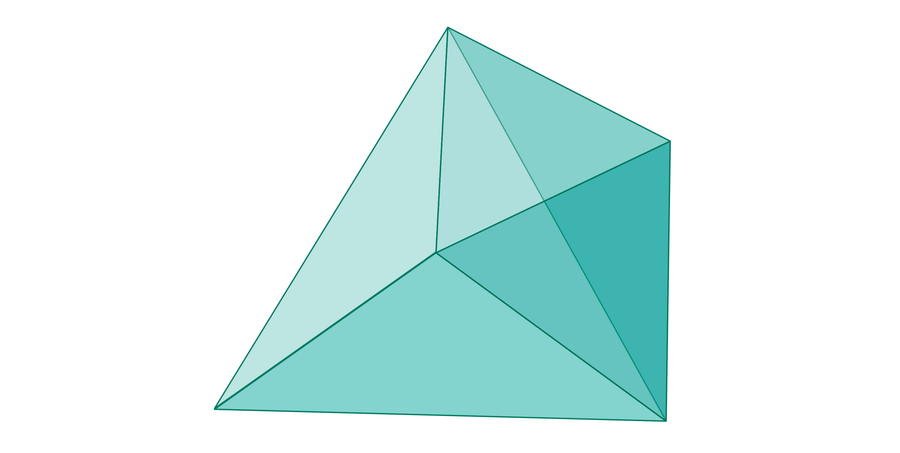
S malou geometrií se ukáže, že tento tvar je přesně polovinou objemu krychle. Tři náhodně vybrané délky tedy budou moci vytvořit trojúhelník přesně polovinu času, jako 1 / (1 × 1 × 2) = 1⁄2.
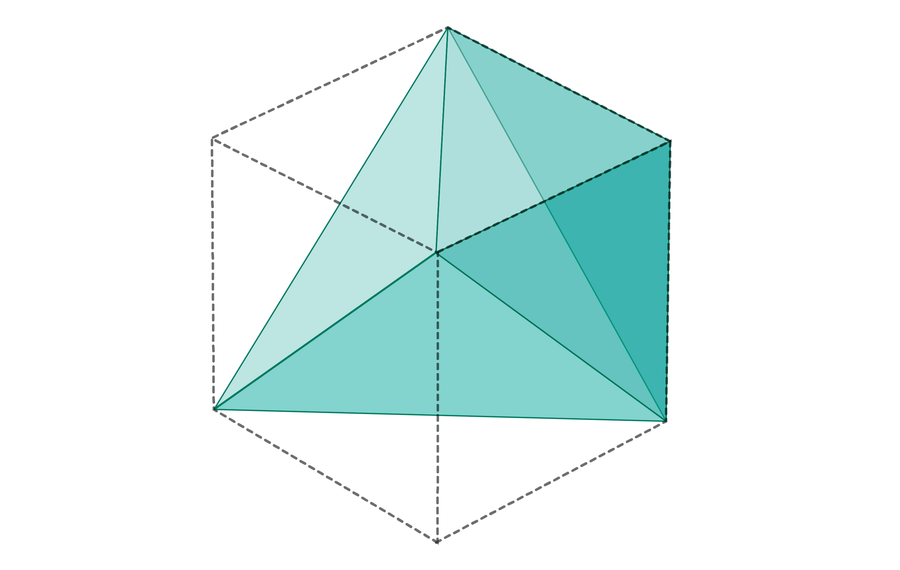
Kam přichází Fibonacci? Předpokládejme, že kolekce libovolného počtu tyčinek je objednána od nejkratší až nejdelší. Pokud mezi nimi žádné tři z nich nevytvoří trojúhelník, musí být délka každé hůlky větší nebo rovná součtu předchozích dvou – jinak by tyto tři hole mohly vytvořit trojúhelník. V sekvenci Fibonacci je každé číslo přesně rovno součtu předchozích dvou. Jinými slovy, každý segment Fibonacciho sekvence je co nejblíže k tomu, aby v něm měl trojúhelník, aniž by byl ve skutečnosti. Podle Treebyho slov: „Pokud se (vyhýbáme se trojúhelníkům), Fibonacciho sekvence se objeví přirozeně.“
Vědci mají pocit, že by měla existovat nějaká cesta přímo z tohoto vhledu k důkazu o vyzvednutí tyčinky. Nemohli však najít. „Doufali jsme, že najdeme něco, co bylo trochu více … intuitivní, ale nemohli jsme formalizovat naše myšlení,“ říká Treeby. Místo toho jejich papír používá integrály k výpočtu přímého výpočtu vysokorozměrných objemu-metoda trochu jako pohledu na oblast uvnitř krychle výše (ale bez vizuálního odkazu). Vědci právě teď nejsou na lovu pro jiný důkaz – ale doufají, že ho někdo najde.
Je čas postavit se za vědu
Než stránku zavřete, musíme požádat o vaši podporu. Vědecký Američan sloužil jako obhájce vědy a průmyslu po dobu 180 let a myslíme si, že právě teď je nejkritičtějším okamžikem v této historii dvou století.
Nežádáme o charitu. Pokud stát se digitálním, tiskem nebo neomezeným předplatitelem Pro Scientific American můžete pomoci zajistit, aby naše pokrytí bylo soustředěno na smysluplný výzkum a objev; že máme zdroje na podávání zpráv o rozhodnutích, která ohrožují laboratoře po celé USA; a že podporujeme jak budoucí, tak pracující vědci v době, kdy se hodnota samotné vědy často nerozpoznala. Kliknutím sem se přihlásíte k odběru.




