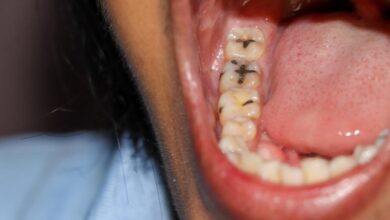
10 nejlepších matematických objevů roku 2025

10 největších matematických objevů roku 2025
Skrytá Fibonacciho čísla, nový tvar a hledání velké sjednocené teorie matematiky patří mezi naše volby pro nejzajímavější zjištění roku

OsakaWayne Studios/Getty Images
V tomto roce jsme zaznamenali několik úžasných pokroků v základní matematice. Výzkumníci učinili průlom v geometrii, topologii, teorii chaosu a dalších. A překvapivé tři z našich 10 nejlepších objevů zahrnují věčně fascinující prvočísla.
Bez dalších okolků, zde jsou některé z nejvíce fascinujících matematických zjištění Scientific American napsal v roce 2025:
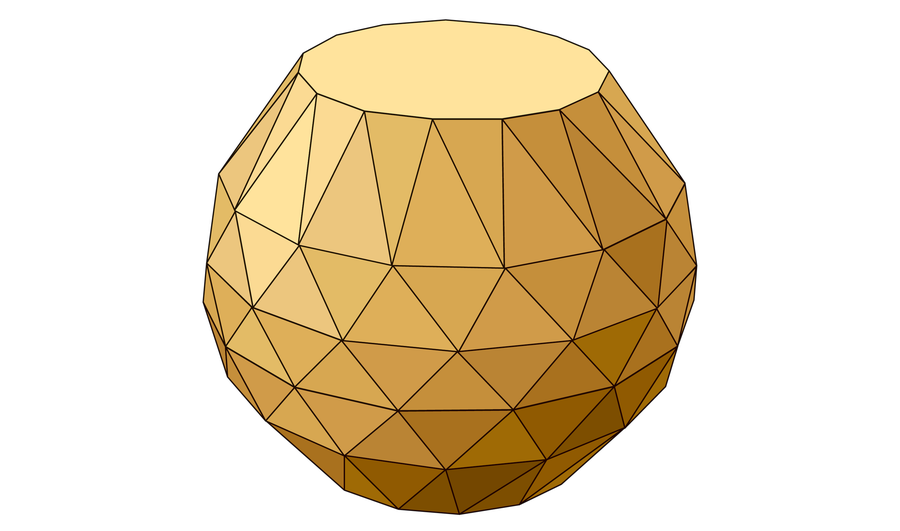
Amanda Montañez; Zdroj: „Konvexní mnohostěn bez Rupertova majetku,“ od Jakoba Steiningera a Sergeje Yurkeviče; arxiv.org/abs/2508.18475v125. srpna 2025 (odkaz)
O podpoře vědecké žurnalistiky
Pokud se vám tento článek líbí, zvažte podporu naší oceňované žurnalistiky předplatné. Zakoupením předplatného pomáháte zajistit budoucnost působivých příběhů o objevech a nápadech, které formují náš dnešní svět.
Nový tvar
Nově nalezený tvar zvaný noperthedron má 90 vrcholů, 240 hran a 152 ploch. Barokní tvar má překvapivou vlastnost, která vyvrací dlouholeté geometrické domněnky: bez ohledu na to, jak jej posunete nebo natočíte, jeden noperthedron nemůže propadnout rovnou dírou v identickém noperthedronu.
Vzory prvočísel
Prvočísla, dělitelná pouze sebou samým a 1, fascinují matematiky odedávna. Objevování nových je obtížné, protože se dostáváte k větším a větším číslům. Ale letos matematici našli soubor pravděpodobnostní vzorce, které řídí distribuci prvočísel. Vzorce zahrnují náhodné chaotické chování a fraktály.
Velká jednotná teorie
„Gargantuovské“ úsilí zahrnující devět matematiků a pět článků o rozsahu téměř 1000 stran v poslední době dokázal geometrický Langlandsův odhad. Dohad spojuje vlastnosti různých Riemannových povrchů, což jsou struktury se souřadnicemi, které mají reálné a imaginární části. Je součástí širšího souboru problémů nazývaných Langlandsův program, který, pokud by byl plně prokázán, mohl poskytnout „velkou jednotnou teorii matematiky“.

Složitost uzlu
Dlouhodobá domněnka tvrdila, že pokud k sobě připojíte konce dvou různých uzlů, bude složitost nového uzlu, který vytvoříte, součtem složitosti jednotlivých uzlů. Ale nedávný objev uzel, který je jednodušší než součet jeho částí tuto domněnku vyvrací.
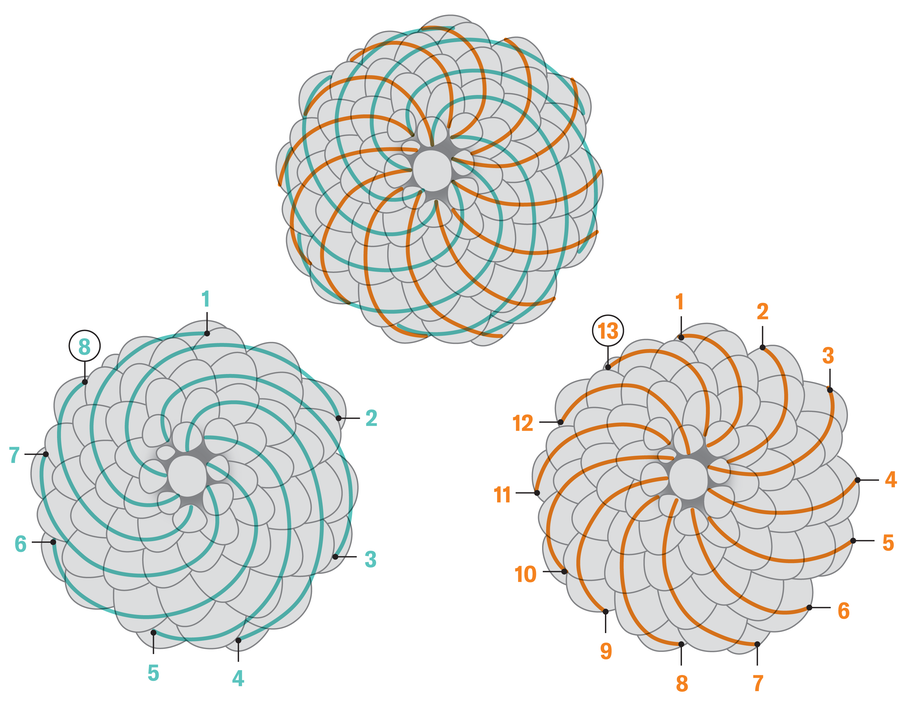
Fibonacciho problémy
Fibonacciho posloupnost, ve které je každý člen součtem předchozích dvou (1, 1, 2, 3, 5, 8, 13, …), se objevuje v celé přírodě. A nyní matematici zjistili, že také poskytuje odpověď na variaci klasického dilema zvaného problém se sběracími tyčemi: Pokud máte několik tyčinek s náhodnými délkami mezi 0 a 1, jaká je pravděpodobnost, že žádné tři z těchto tyčinek nevytvoří trojúhelník?
Detekce Primes
Největší známé prvočíslo, 2136,279,841 − 1, má 41 024 320 číslic, ale matematici nejsou spokojeni – chtějí najít ještě větší prvočísla. Tento rok identifikoval tým nový přístup k hledání neobjevených prvočísel. Strategie zahrnuje oddíly nebo způsoby, jak se čísla mohou sčítat, aby vytvořila další čísla.
125-letý problém vyřešen
V roce 1900 matematik David Hilbert představil řadu hlavních nevyřešených problémů. Jedním z nich byl cíl určit co nejméně matematických předpokladů za fyzikálními zákony. Výzkumníci později tento úkol rozdělili na dílčí cíle a letos matematici tvrdili, že jeden z nich splnili: sjednotili tři fyzikální teorie k vysvětlení pohybu tekutin. Pokud se úspěch potvrdí, bude významný krok k vyřešení Hilbertova šestého problému.
Jen Christiansen; Zdroj: “Animation of Dudeney’s Dissection Transforming an Equilateral Triangle to A Square,” od Marka D. Meyersona (odkaz)
Trojúhelníky až čtverce
Na kolik kusů musíte rozřezat trojúhelník, abyste ho mohli přestavět na čtverec? V roce 1902 našel čtenář novin způsob, jak to udělat se čtyřmi kusy, ale od té doby se to nikomu nepodařilo udělat v méně kusech. Letos vědci konečně dokázali, že a trojúhelník nařezaný na méně než čtyři kusy nelze změnit na čtverec.
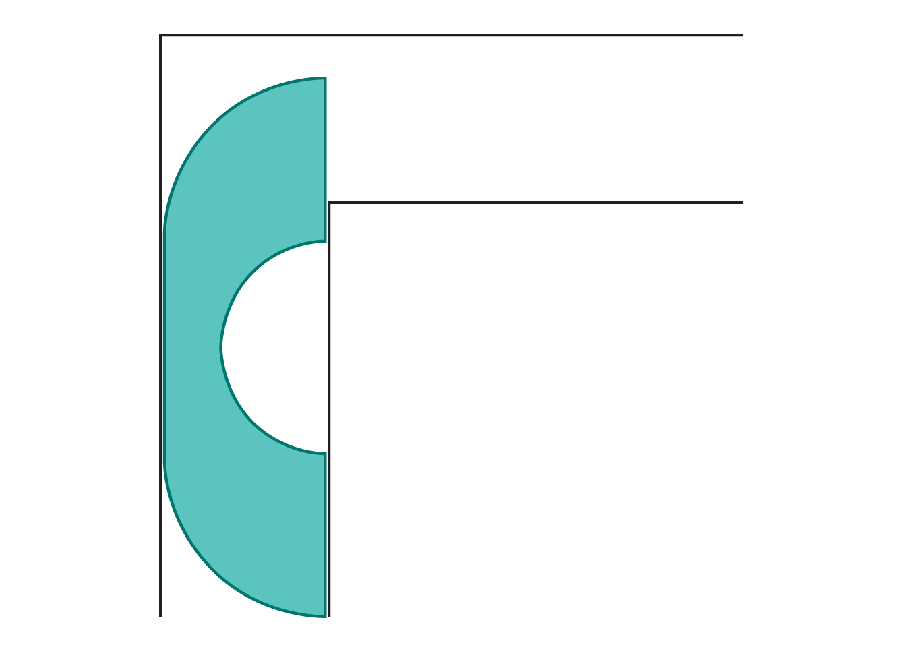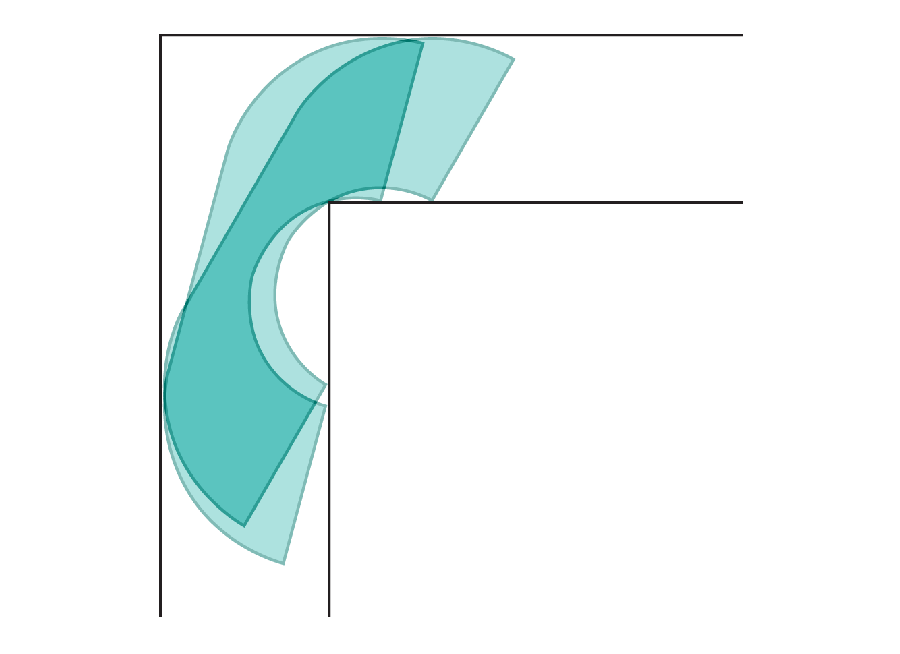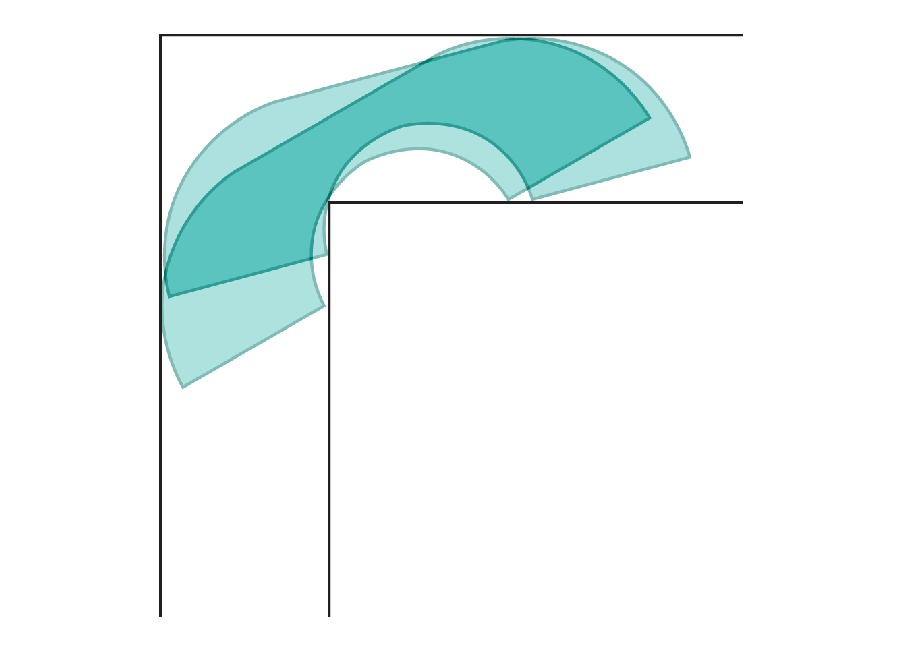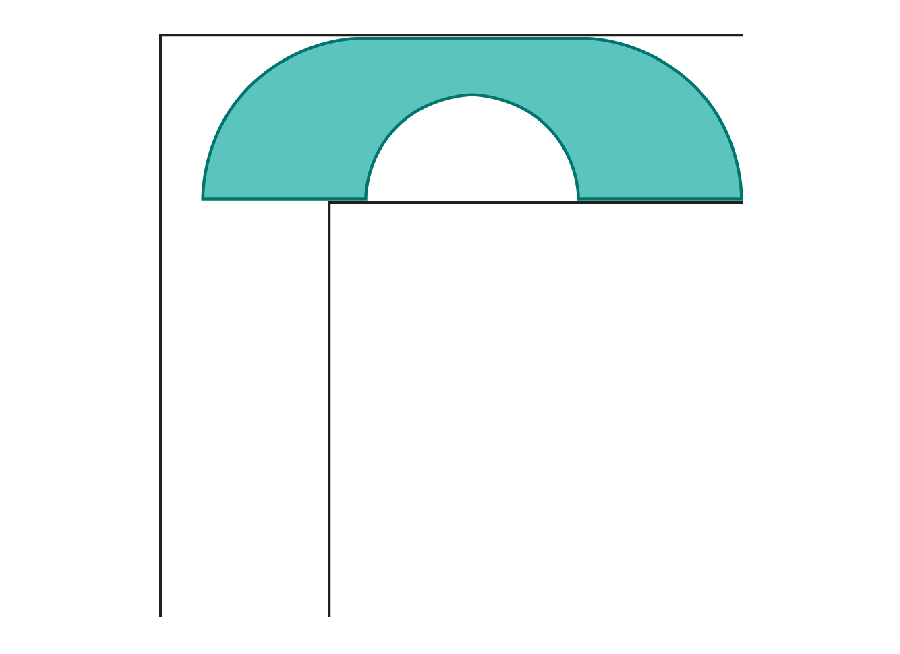
Amanda Montañez; Zdroj: “On Moving a Sofa Around a Corner,” Joseph L. Gerver, in Věnováno geometriisv. 42, č. 3; června 1992 (odkaz)
Pohyblivé pohovky
Každý, kdo se stěhoval domů, může ocenit dilema pokusit se umístit velkou pohovku za roh. Matematici tuto otázku formálně rozpoznali asi před 60 lety, když ji nazvali „problém se stěhováním pohovky“: Jaký je největší tvar, který se dokáže otočit do pravého úhlu v úzké chodbě, aniž by se zasekl? Vědci nyní našli řešení.
Chytání prvočísel
Dalším průlomem na přední straně je a nová metoda pro odhad, kolik prvočísel existuje v libovolném daném rozsahu čísel. Strategie nejprve spoléhá na eliminaci všech čísel, která jsou násobky jiných prvočísel, a proto nemohou být prvočísla sama o sobě. Potom zohledňuje čísla, která jsou ze seznamu vyškrtnuta více než jednou. Autoři studie také objevili hranici toho, jak přesný může být jakýkoli odhad tohoto druhu, což ukazuje, že základní záhady prvočísel zůstanou nepolapitelné, alespoň prozatím.
Je čas postavit se za vědu
Pokud se vám tento článek líbil, rád bych vás požádal o podporu. Scientific American sloužil jako obhájce vědy a průmyslu již 180 let a právě teď může nastat nejkritičtější okamžik v této dvousetleté historii.
Byl jsem a Scientific American předplatitel od mých 12 let a pomohlo mi to utvářet můj pohled na svět. SciAm vždy mě vzdělává a těší a vzbuzuje úctu k našemu obrovskému, krásnému vesmíru. Doufám, že to udělá i vám.
Pokud vy přihlásit se k odběru Scientific Americanpomáháte zajistit, aby se naše pokrytí soustředilo na smysluplný výzkum a objevy; že máme zdroje na podávání zpráv o rozhodnutích, která ohrožují laboratoře v USA; a že podporujeme začínající i pracující vědce v době, kdy hodnota samotné vědy příliš často zůstává nepoznaná.
Na oplátku získáte zásadní zprávy, strhující podcastyskvělá infografika, nepřehlédnutelné newsletteryvidea, která musíte vidět, náročné hrya nejlepší vědecké psaní a zpravodajství. Můžete dokonce darovat někomu předplatné.
Nikdy nebyl důležitější čas, abychom vstali a ukázali, proč na vědě záleží. Doufám, že nás v této misi podpoříte.