Jak chyba v kultovní klasické hře Doom vyvolala nové uznání pro Pi

Každý dělá chyby – a někdy tyto chyby mohou vést k překvapivým objevům. Na začátku 90. let, když programoval počítačovou hru Doom, herní vývojář John Carmack nastavil hodnotu pí (π) ručně – a jako opravdový pitomec zapsal číslo z paměti na deváté desetinné místo: 3,141592657.
Všímáte si na té postavě něčeho divného? Poslední číslice je špatná. Místo toho by mělo být číslo 3,141592654. (Pí je často zkráceno bez zaokrouhlení, v takovém případě by bylo deváté desetinné místo vyplněno 3, ale zaokrouhluje se na 4, protože následující číslice je 5.)
Naštěstí má tato chyba na hru malý dopad. Ve hře Doom, jedné z prvních stříleček z pohledu první osoby s trojrozměrnou grafikou, se ujmete role vesmírného mariňáka, který kvůli neúspěšnému experimentu s teleportací skončí na měsíci Marsu, kde bojuje s démony a zombie. Hra má skvělý příběh, ale hroznou grafiku. Není to kvůli nesprávné hodnotě pí, ale spíše odrazem toho, jak malý výpočetní výkon byl k dispozici v 90. letech.
O podpoře vědecké žurnalistiky
Pokud se vám tento článek líbí, zvažte podporu naší oceňované žurnalistiky předplatné. Zakoupením předplatného pomáháte zajistit budoucnost působivých příběhů o objevech a nápadech, které formují náš dnešní svět.
Přesto tato chyba inspirovala amerického inženýra Luka Gotszlinga, aby prozkoumal možné důsledky nesprávného naprogramování pi ve větším měřítku ve hře – nápad, který představil na hackerská konference v roce 2022.
Když se Pi v počítačové hře mýlí
Protože Doom je počítačová hra s otevřeným zdrojovým kódem, můžete si stáhnout kód – a upravit jej. Gotszling to udělal a testoval, co by se stalo, kdyby změnil naprogramované hodnoty pí.
Výsledky mohou způsobit, že se divák cítí trochu nevolně. Když Gotszling například nastavil π = 3, rozpixelovaný svět Doom se zdeformoval a stěny a sloupy se pohybovaly neočekávaným způsobem. Přesto byla hra hratelná.
Když bylo pí nastaveno na hodnotu Eulerova čísla, 2,718…, podivnost zesílila. Jak se hráč pohyboval přímo v herním světě, okolní předměty se pohybovaly na různé strany. Nepřátelé se mohli z ničeho nic objevit a zase zmizet. „S dostatečnou intoxikací to můžete znovu vytvořit,“ vtipkoval Gotszling ve své prezentaci.
Věci se opravdu zhoršily, když nastavil hodnotu p⁄2 pro pí. Stěny by blikaly a zmizely. Neviditelné překážky brání hráči v pohybu. Hra v tomto stavu nebyla nijak zvlášť zábavná.
Pi není vždy 3,14159…
Proč je pí tak silné? Abychom na to mohli odpovědět, musíme se hlouběji zamyslet nad důsledky změny pí.
Původně bylo pí definováno jako poměr obvodu kruhu k jeho průměru. V našem každodenním světě předpokládáme, že kruhy jsou kulaté. Ale v užším matematickém smyslu je kruh definován všemi body, které jsou stejně vzdálené od společného středu. V plochém, dvourozměrném světě, kde jsou vzdálenosti definovány jako nejkratší přímky, je kruh kulatý. To znamená, že hodnota pí se může změnit.
Představte si například, že stojíte v centru Manhattanu. Pokud chcete zjistit, která místa jsou od vás vzdálená přesně jeden kilometr, tvar, který můžete vytvořit, již nebude kulatý. To proto, že nemůžete procházet zdmi. Místo toho musíte sledovat šachovnicové rozložení ulic. Kruh má čtvercový tvar v „manhattanské metrice“, jak se tomu říká v matematickém žargonu. A pokud v této souvislosti definujete pí jako poměr obvodu k průměru, číslo nabývá úplně jiných hodnot: v manhattanské metrice je pí přesně 4.
Když se podíváte pozorně, hodnota pí v našem světě není přesně 3,14159…. Místo toho poměr obvodu k průměru nabývá jiné hodnoty – a co je ještě horší, tato hodnota se mění!
Pokud stojíte na severním pólu a díváte se na všechna místa přesně 1000 kilometrů od vás, například tyto body tvoří kruh na povrchu koule – ale její obvod je díky zakřivení Země menší než obvod kruhu na rovném povrchu. Čím více se blížíte k rovníku, tím je tento efekt silnější a odpovídající hodnota pí se stále více odchyluje od obvyklých 3,14159….
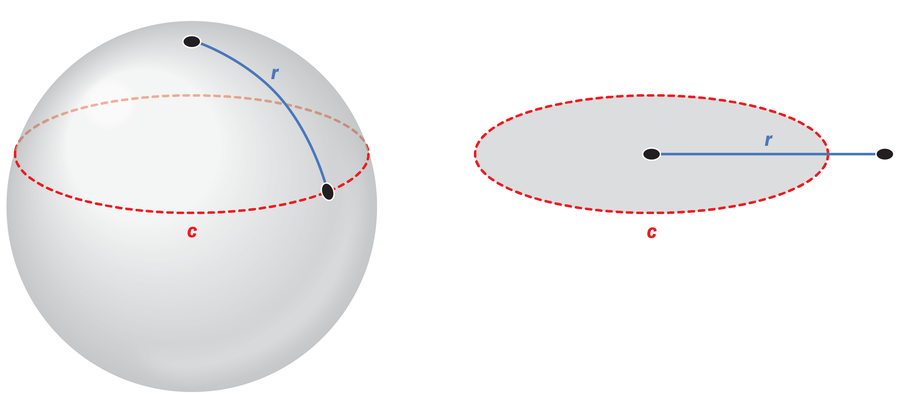
Nová hodnota pí proto není konstantní, ale závisí na poloměru kružnice. A to neplatí jen v případě kulového povrchu. Jakýkoli typ zakřiveného povrchu poskytuje proměnné hodnoty pro pí.
Matematici označují takovéto zakřivené světy jako „neeuklidovské“ geometrie. (Před více než 2000 lety učenec Euclid vyložil pravidla geometrie, kterou se většina z nás naučila ve škole – myšlenky, které platí pouze pro plochý svět.)
Vytvoření Trippy Vision of Doom
Svérázná krajina Gotszling vytvořená vyladěním zdrojového kódu Dooma je něco úplně jiného. Abychom to pochopili, musíme se vrátit do 90. let 20. století: do doby, kdy každá aritmetická operace spotřebovávala obrovské množství zdrojů. Aby programátoři tuto výzvu zvládli, snažili se předem určit možné výpočty a uložit je do „vyhledávacích tabulek“.
Při vývoji 3D grafiky pro počítačovou hru hrají důležitou roli trigonometrické funkce jako sinus, kosinus a tangens. Mohou být použity k popisu toho, jak se předměty pohybují prostorem v průběhu času. Aby se ušetřil výpočetní výkon, vývojáři Doom předem vypočítali důležité hodnoty trigonometrických funkcí pro různé úhly a uložili je do vyhledávacích tabulek. A tady vstupuje do hry pí: musíte vynásobit úhel ve stupních pí, abyste získali odpovídající hodnotu v radiánech, kterou počítač používá.
Pokud by tedy Gotszling použil hodnotu pí, která byla příliš malá, úhly by byly převedeny nesprávně. Protože vývojáři ukládají pouze konečný počet úhlů, vytvořil vyhledávací tabulky s hodnotami, které již nezahrnují úplné otočení: Místo popisu prostředí, ve kterém se objekt znovu objeví na stejném místě po otočení o 360 stupňů, k tomu dojde po výrazně menším úhlu. Výsledkem je, že v extrémních situacích předměty náhle z ničeho nic zmizí nebo se znovu objeví.
Doom svět, který Gotszling vytvořil, je neuvěřitelně zvláštní. Nicméně je to pěkný způsob, jak přimět lidi, aby přemýšleli o matematice a hodnotě – v každém smyslu – pí. Jedna malá chyba vývojáře hry vyvolala mnohem větší experiment s podivným kruhovým číslem.
Tento článek se původně objevil v spektrum vědy a byl reprodukován se svolením.