Jak matematika zamíchacích karet téměř snížila online pokerovou říši

Pokud jste někdy zamíchali balíček hracích karet, pravděpodobně jste vytvořili jedinečný balíček. To znamená, že jste pravděpodobně jediný člověk, který karty uspořádal přesně v tomto pořadí. Ačkoli toto tvrzení zní neuvěřitelně, je to skvělá ilustrace toho, jak rychle se může velká čísla vplížit do každodenních situací – s občas náročnými důsledky, protože vývojáři online pokerové hry bolestně objevili na konci 90. let.
Matematika míchání karty je docela snadné vysvětlit. Chcete -li vypočítat, kolik uspořádání 52 hracích karet může mít, musíte projít všemi možnými míchání. Takže logicky je jedna z 52 karet umístěna nahoře a jakmile je to určeno, existuje pouze 51 možností pro kartu pod ní. Další karta má pouze 50 možných možností atd. Paluba 52 karty lze proto uspořádat v 52 × 51 × 50 × … × 2 × 1 = 52! odlišně.
Pokud uděláte násobení a obříznete odpověď, získáte číslo s 67 nuly. To je více než kvadrilionkrát tolik způsobů, jak uspořádat tyto karty, jako jsou atomy na Zemi.
O podpoře vědecké žurnalistiky
Pokud se vám tento článek líbí, zvažte podporu naší oceněné žurnalistiky předplatné. Zakoupením předplatného pomáháte zajistit budoucnost působivých příběhů o objevech a myšlenkách, které dnes formují náš svět.
Takže jasně existuje mnoho, mnoho různých způsobů, jak uspořádat 52 hracích karet. A přesto zjistit, jak je pravděpodobné, že jiná osoba na světě náhodně vytvoří stejnou sekvenci karet zamícháním, nestačí jednoduše vypočítat 1/52! Toto číslo jednoduše ukazuje, jak je pravděpodobné získat jeden velmi specifický zamíchání karet.
Je třeba zvážit jemnější otázku: Jak by bylo pravděpodobné, že by to bylo, aby všichni dva nebo více lidí na světě náhodně zamíchali palubu karet stejným způsobem?
Mimořádná vzácnost každého zamíchání
Tato otázka připomíná Narozeninový paradox. Funguje to podle stejného principu: Je poměrně nepravděpodobné, že student ve třídě má k narozeninám k danému datu – ve skupině 30 lidí je pravděpodobnost 1 – (364 /365)30≈ 7,9 procenta. Pravděpodobnost, že se dva studenti narodí ve stejný den, je však více než 70 procent. Důvodem této zjevné nesrovnalosti je to, že lidé obvykle podceňují, kolik možných párů studentů existuje. Z 30 studentů lze vytvořit 435 párů. Pravděpodobnost, že se každý pár studentů narodil v jiný den, pak se nezdá tak vysoká.
Pokud chcete zjistit, jak je pravděpodobné, že náhodně zamíchá palubu karet stejným způsobem jako jakákoli jiná osoba na světě, existuje několik způsobů, jak to udělat. Jedním z nich je nejprve vypočítat pravděpodobnost opačné události a poté odevzdat tento výsledek z 1.. To znamená, že nejprve prozkoumáte, jak je pravděpodobné, že všichni lidé na světě vytvářejí při míchání zcela nové uspořádání: první osoba má pravděpodobnost 1, druhá pravděpodobnost (52! – 1) / 52!, Třetí z (52! – 2) / 52!, A tak on. Poté odečtěte tento výsledek z 1.
Pokud na světě je osm miliard lidí, pravděpodobnost, že několik lidí vytvoří stejný zamíchání karet, lze vypočítat takto:
Problém je v tom, že moje kalkulačka (nebo spíše online program Wolfram | alfa) selže, když se pokusím vyhodnotit tento vzorec. Proto se musím spoléhat na velmi hrubý odhad této pravděpodobnosti:
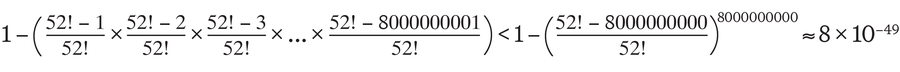
To znamená, že pravděpodobnost, že dva nebo více lidí na světě vytvoří stejný balíček karet, je menší než 0,0000 … 08 procent – číslo, které se od 0 na 47. desetinném místě odchyluje pouze.
S touto ilustrací jsem doufám, že jsem všechny přesvědčil, že je nesmírně nepravděpodobné, že by několik lidí na světě náhodně vytvořilo stejný balíček karet zamícháním. Ale pravděpodobně jste ve svém životě mnohokrát zamíchali karty, nejen jednou. Jak se tedy výsledek změní, pokud předpokládáme, že každý člověk zamíchá přibližně 100 paluby karet za jejich život? Nahrazením osmi miliard v předchozím odhadu s 800 miliardami zjistíme, že pravděpodobnost v tomto případě je menší než 8 × 10−43 procento.
Jinými slovy, šance se moc nemění. I když každý člověk na světě zamíchá palubu karet 100krát, je velmi nepravděpodobné, že by se stejný balíček objevil dvakrát.
Pokud vezmeme v úvahu každého člověka, který žije nebo někdy žil na Zemi – podle některých odhadů, o 117 miliard Lidé – každý z nich zamíchal palubu karet asi 100krát (což je nepravděpodobné, vzhledem k tomu, že náš druh neměl hrací karty příliš dlouho), pak pravděpodobnost, že stejné uspořádání bylo vytvořeno vícekrát, je menší než 1,7 × 10−40 procento.
To je jasné: je opravdu velmi nepravděpodobné, že by dva lidé v celé historii lidstva někdy zamíchali palubu karet stejným způsobem – alespoň za předpokladu, že zamíchali karty velkou péčí. To ukazuje, jak Big 52! je a jak nesmírně mnoho možností existuje pro uspořádání 52 karet.
Přečtěte si je a pláč
Rozsáhlost 52! Je nejen inspirativní pro uvažování – také představoval některé významné praktické problémy pro vývojáře online her. Online poker může zahrnovat velké částky peněz, takže je důležité, aby tyto hry byly co nejbezpečnější a spravedlivější. Jakékoli nedostatky nebo mezery mohou být podvodníci využívány nebo použity dům proti hráčům.
Digitální karty by měly být dobře zamíchané a náhodně řečeno, stejně jako skutečné. V ideálním světě by algoritmus náhodně vybral uspořádání z 52! možné paluby. Žádný počítač však nemá dostatek paměti pro vyhodnocení všech těchto možností a dokonalý generátor náhodných čísel dosud neexistuje. Vývojáři se proto obecně spoléhají na algoritmy, které simulují míchání karty.
Na konci 90. let dodala vývojová platforma ASF software několik poskytovatelů online pokeru, jako je Planet Poker, s algoritmy zamícháním karet. Platforma dokonce zveřejnila algoritmus na svých webových stránkách jako důkaz, že hra byla spolehlivě naprogramována. A tento příspěvek upoutal pozornost některých zaměstnanců na spolehlivé softwarové technologie, IT společnosti. „Jakmile jsme viděli algoritmus promíchání, začali jsme mít podezření, že by mohl být problém. Malé vyšetřování prokázalo, že tato intuice byla správná,“ několik zaměstnanců napsal v příspěvkuNa webových stránkách vývoje softwaru.
Algoritmus začal objednávaným balíčkem karet a poté v několika krocích vyměnil dvě karty. K tomu program použil generátor náhodných čísel propojený s časem systému počítače. Na této metodě však existuje několik omezení. Za prvé, mechanismus výměny byl implementován tak, že byla upřednostňována určitá uspořádání karet a častěji se objevila než jiné. Pro další systém spojuje generování počtu s počtem sekund, které prošly od půlnoci, a resetuje jednou denně, což dále omezuje možné náhodné hodnoty. Tímto způsobem by mohlo být vytvořeno pouze asi 86 milionů ujednání, objevil tým spolehlivých softwarových technologií.
Programátoři si pak uvědomili, že protože systém je svázán s hodinami, aby se randomizoval své míchání, bylo možné uspořádat karty tím, že zohledňujeme tento časoměřič. Jednoduše synchronizace jejich vlastního programu do systémových hodin snížila možnosti na pouhých 200 000 potenciálních balíčků, které by algoritmus mohl generovat. „Po tomto tahu je systém náš, protože hledání této malé sady míchání je triviální a lze jej provádět na PC v reálném čase,“ napsali. Připomeňme, že to bylo zpět v 90. letech, kdy byly počítače výrazně méně silné než dnes.
Zaměstnanci spolehlivých softwarových technologií informovali tyto slabiny vývojářům algoritmu, kteří je okamžitě revidovali. Dnes mnoho online pokerových stránek používá algoritmus Fisher -Yates, nazývaný Knuth Shuffle (který zní nádherně jako tanec). Je snadné implementovat a poskytovat uspokojivé výsledky.
Tyto algoritmy jsou samozřejmě omezeny jinými způsoby – generátory randomů prostě nejsou dost dobré na to, aby lidé mohli dělat se skutečným balíčkem. Ale ani ten nejhorší lidský prodejce nemůže pokaždé poskytnout dokonalou ruku.
Díky podcastu německého jazyka Nerds v práci Podcast pro inspiraci mě psát o tomto pokerovém algoritmu z 90. let.
Tento článek se původně objevil v Spektrum vědy a byl reprodukován se svolením.