Laureáta Abel Masaki Kashiwara změnila, jak Algebra splňuje analýzu

V březnu letošního roku japonský matematik Masaki Kashiwara zjistil, že za zoom volání, že mu byla udělena cenu Abela, jedna z nejvyšších vyznamenání matematiky, za „jeho základní příspěvky k algebraické analýze a teorii reprezentace“.
Dr. Kashiwara začal rozvíjet části své Abel-vyhrávající práce, když mu bylo 23. Je mu nyní 78.
V té době, zapsaný jako postgraduální student na Tokijské univerzitě v Japonsku, začal pracovat s D-Modules-způsob, jakým mohou matematici studovat systém částečných diferenciálních rovnic pomocí nástrojů algebry. Tyto rovnice se běžně vyskytují napříč vědami.
V roce 1980 použil Dr. Kashiwara svou teorii D-modulů k prokázání korespondence Riemann-Hilberta-jeden z 23 slavných problémů, které představuje německý matematik David Hilbert v roce 1900. (Tři Hilbertovy problémy zůstávají dodnes nevyřešeny.)
Takový byl dopad této práce, že „Kashiwara mohl (dokonce i) vyhrávat medaili polí již na Mezinárodním kongresu matematiků… v roce 1982,“ Dr. Pierre Schapira, francouzský matematik, který spolupracoval s Kashiwarou více než pět desetiletí,, více než pět desetiletí. napsal v dubnu letošního roku. Medaile Fields je další prestižní cenou v matematice, ale je vyhrazena těm mladším 40 let.
V roce 1982 odešla medaile Alainovi Connesovi, Williamovi Thurstonovi a Shing-Tung Yau. Když Dr. Kashiwara nevyhrál, Dr. Schapira spekulovala, že „protože jeho práce byla příliš inovativní na to, aby byla v té době pochopena“.
A právě začal.
Korespondence Riemann-Hilbert
Diferenciální rovnice nám pomáhají popsat, jak se jedno množství mění s ohledem na jiné. Například takovou rovnici lze použít k popisu toho, jak se rychlost vozidla mění vůči času. Řešení této rovnice může pomoci říci, zda se vůz v určitém okamžiku a tím, kolik toho a tím, jak moc.
Riemann-Hilbertova korespondence je o konkrétním typu diferenciálních rovnic nazývaných lineární parciální diferenciální rovnice.
Představte si, že pečíte dort. Když ji trouba zahřívá z vnějšku, teplo se rozprostírá uvnitř dortu a různé části dortu teplé při různých rychlostech. Pokud jste to chtěli popsat, musíte vědět, jak se teplota v čase mění a jak se mění v různých bodech uvnitř dortu. Částečná diferenciální rovnice je matematický způsob, jak sledovat všechny tyto změny najednou.
Při práci na matematické rovnici je možné se setkat s řešením, které není dobře definováno. Například řešení rovnice y = 1/x není definován pro x = 0. Takové body se nazývají singularity.
Částečné diferenciální rovnice mají také singularitu.
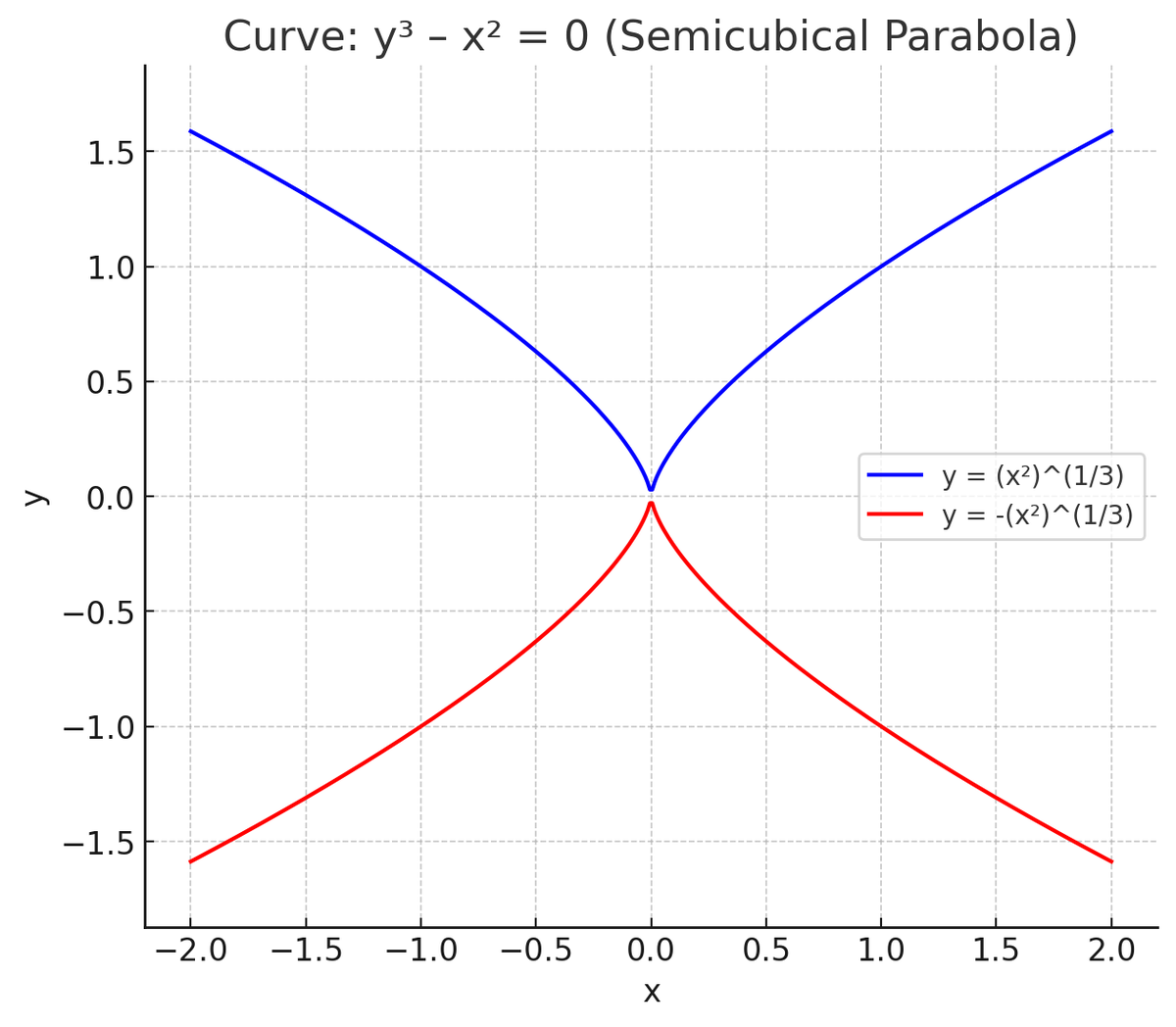
Graf zobrazující singularitu při (0, 0) pro funkci y^3 – x^2 = 0. | Fotografický kredit: Obrázek vytvořený pomocí chatgpt 5
A pokud sledujete řešení částečné diferenciální rovnice pro body kolem singularity, narazíte na efekt zvaný monodromy. Představte si točité schodiště, kde je každý krok bodem, kde lze rovnici vyřešit. Ve středu spirály leží singularita.
Protože řešení leží podél spirálového schodiště, otočení jednoho úplného otočení schodiště vás nevrátí do bodu, kdy jsme začali. Místo toho budete vyšplhat na úroveň vyšší nebo o úroveň nižší. Je to jako monodromie. Konkrétně je monodromie, když se roztoky částečné diferenciální rovnice kolem bodu chovají odlišně, když se k němu vrátíme po smyčce kolem singularity.
Když Hilbert navrhl Riemann-Hilbertovu korespondenci, věděl, že vzhledem k částečné diferenciální rovnici člověk může identifikovat jeho singularity a monodromie. Přemýšlel, jestli je opak pravdivý: že vzhledem k singularitě a monodromii kolem něj by bylo možné určit odpovídající rovnici?
Belgický matematik Peter Deligne poskytl důkaz o korespondenci Riemann-Hilberta v roce 1970. O deset let později dva matematici-Zoghman Mebkhout a Dr. Kashiwara-nezávisle to prokázalo pro nastavení obecnější než Deligne.
Důkaz Dr. Kashiwary zahrnoval teorii D-modulů.

„Nový horizont“
Práce Dr. Kashiwary byla součástí většího projektu, který inicioval jeho poradce Mikio Sato, japonský matematik připisoval v roce 1959 zahájením oblasti algebraické analýzy.
Algebra je pole matematiky, které se zabývá proměnnými (např. x a y) a vztahy mezi nimi. Analýza je pole, které se snaží poskytnout teoretický základ pro počet. Analytici se mimo jiné zabývají tím, jak řešit diferenciální rovnice.
I když jsou ve vědách běžné, je známo, že diferenciální rovnice je velmi obtížné vyřešit. Ve skutečnosti, s výjimkou některých z nejjednodušších případů, neexistují žádné explicitní vzorce, které by je praskly.
Algebraická analýza Sato byla pokusem obejít potřebu vyřešit jednotlivé diferenciální rovnice. Místo toho si přál použít nástroje algebry ke studiu, jak se chovají určité druhy částečných diferenciálních rovnic.
To by pomohlo matematikům studovat všechna řešení systému částečných diferenciálních rovnic spíše než jednotlivých řešení, uvedl Arvind Nair, matematik na Tata Institute of Fundamental Research, Mumbai.
„Pohybující se otázky (analýzy) na algebru umožňují použití nástrojů algebry“ pro studium dílčích diferenciálních rovnic, „které jsou často velmi silné,“ dodal.
Algebraická analýza se také snažila překlenout dvě domény matematiky – algebry a analýza – dříve považovaná za nezávislé. Výsledkem je, že vědci mohou řešit problémy z jedné domény pomocí nástrojů druhé.
V a 2024 PapírSchapira, spolupracovník Dr. Kashiwary, nazval tento pokrok „nový horizont v matematice“.
Dr. Kashiwara vzal Satoův sen vpřed, když začal pracovat na D-Modules jako student. Podle Dr. SchapiraKashiwarova práce na D-modulech konečně dala matematikům „nástroje k léčbě obecných systémů lineárních částečných diferenciálních rovnic, na rozdíl od jedné rovnice s jedním neznámým“.
To znamená, že místo toho, aby se pokusili vyřešit jednu částečnou diferenciální rovnici podrobně, D-moduly umožnily matematikům studovat, jak se třídy takových rovnic chovaly v různých podmínkách.
Kashiwara ve svém úsilí v jeho úsilí přepracoval korespondenci Riemann-Hilberta jako korespondenci mezi D-moduly a matematickými objekty zvanými zvráceně. Ten je způsob, jak reprezentovat systémy roztoků polynomiálních rovnic. Polynomiální rovnice je algebraický výraz jako x2 + y2 = 0.
„To lze považovat za slovník mezi dvěma druhy (matematických) objektů,“ řekl Dr. Nair.
Hilbertova verze tohoto slovníku zahrnovala částečné diferenciální rovnice a sbírku singularit a monodromie kolem nich.
Reformulace Dr. Kashiwary také rozšířila rozsah korespondence. Podle Apoorva Khare, docentka matematiky na Indickém vědeckém institutu Bengaluru, „Původní nastavení problému bylo mnohem omezenější než ten, který Kashiwara vyřešil.“

Teorie reprezentace
Asi deset let poté, co Dr. Kashiwara prokázal korespondenci Riemann-Hilberta, udělal další velký průlom, tentokrát v odvětví matematiky zvané teorie reprezentace. Ačkoli patří matematice, teorie reprezentace je také velmi důležitá ve fyzice – zejména kvantová fyzika. Fyzici ve skutečnosti jej často používají jako jazyk k popisu chování základních částic, jako jsou elektrony a fotony.
Teorie reprezentace bere komplikované matematické objekty a vyjadřuje je z hlediska jednodušších. Dobrým příkladem jsou skupiny. V matematice je skupina sada všech různých způsobů, jak můžete změnit polohu objektu – otočením, převrácením nebo pohybem kolem. Každá taková změna se nazývá prvek skupiny.
Skupiny mohou být velmi obtížné studovat, protože nesou tolik informací. Aby se usnadnili zvládnout, teorie reprezentace je přeměňuje na matrice, což jsou obdélníkové mřížky čísel nebo symbolů. Teorie nabízí pravidla, takže každý prvek skupiny odpovídá konkrétní matici.
Tuto myšlenku reprezentace s maticemi lze rozšířit i na další matematické objekty. Jedním z důležitých příkladů je kvantová skupina vytvořená matematiky a fyziky v 80. letech. To je místo, kde se Dr. Kashiwara podařilo značku.
Posun na graf
V roce 1990 vynalezl Dr. Kashiwara Crystal Bases, nový způsob, jak reprezentovat kvantové skupiny. (MIT matematika profesor George Lusztig také nezávisle vynalezl křišťálové základny současně.)
Zvažte dvourozměrný prostor, jako je graf s x a y-osy. Bod v tomto grafu může být reprezentován jako vektor: šipka, která začíná od původu a končí v bodě. Tyto vektory mohou být vyjádřeny jako kombinace pohybů podél osy x a y. Například můžete dosáhnout (5, 3) od (0, 0) přesunutím 5 jednotek na ose x následované 3 jednotkami na ose y.
Matematici nazývají tyto jednotné hnutí „základny“. Podle Dr. Khare, Kashiwara změnil základ kvantových skupin na grafy. Byl to významný úspěch, protože vytvořil „kombinatoriální nástroj, který umožnil řešení mnoha problémů (kvantových skupin) v teorii reprezentace“, za biografii Kashiwara na webových stránkách Abel Prize.
Dr. Khare dodal, že tato technika usnadnila „výpočty na těchto objektech“ a že přinesla „komplexnější informace o kvantových skupinách“.

Matematici po celém světě často používají objevy Dr. Kashiwary k posunutí hranic jejich disciplín. Například Dr. Nair, matematik TIFR Bombai, uvedl, že ve své práci používá formulaci „korespondence Riemann-Hilbert Korespondence“ z „Riemann-Hilbertovy korespondence“. Dr. Nair pracuje na teorii reprezentace a algebraické geometrii; Ten používá algebraické techniky k řešení problémů v geometrii.
Možná největší přínos Dr. Kashiwary je budování mostů mezi různými doménami matematiky. Například jeho práce na modulech na modulech přemostí studium diferenciálních rovnic s algebrou a topologií, studium prostorů, které se nezměnily za určitých druhů deformací.
Přitom umožňuje matematikům řešit problémy v jedné doméně s nástroji vypůjčenými z jiné domény – poněkud jako to, jak používání teflonových povlaků, původně vyrobených k ochraně letadel, vede k dietě s menším olejem na vaření.
V 78 letech Dr. Kashiwara stále staví tyto mosty pro matematiku.
Sayantan Datta je členem fakulty na Krea University a nezávislým vědeckým novinářem. Autor děkuje Pierre Schapira (Sorbonne University) a Kn Raghavan, Rishi Vyas a Vivek Tewary (All At na Krea University) za jejich vstupy.