Parrondo’s Paradox vysvětluje, jak mohou zvítězit dvě kombinované strategie prohry

Matematický paradox ukazuje, jak může kombinace proherních strategií přinést výhru

Podle Manon Bischoffová upravil Daisy Yuhas

V roce 1996 vytvořil španělský fyzik Juan Parrondo neuvěřitelný objev: někdy mohou být dvě hry, z nichž každá končí prohrou jednotlivě, spojeny do vítězné strategie. Tento paradox není pouhou matematickou kuriozitou – je vědecky užitečný. Pomáhá to vysvětlit různé životní historie slizniček a mohl přispět k novému strategie léčby rakoviny.

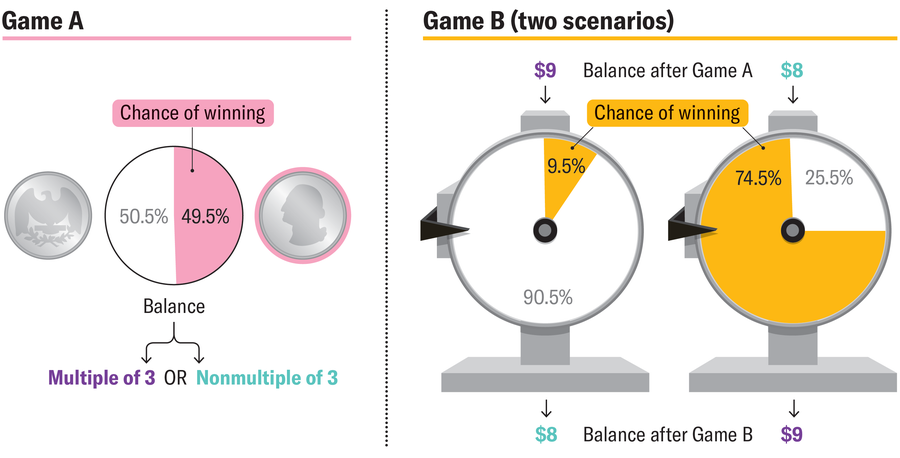
Abychom pochopili tento paradox, musíme si představit situaci, ve které hrajete dvě hry s nějakými velmi specifickými parametry. Představme si například, že první hra „A“ zahrnuje hod mincí. Mince má v tomto případě rozložení hmotnosti mírně pozměněné tak, aby dopadla přednostně na jednu stranu s pravděpodobností 50,5 procenta. Nyní předpokládejme, že hra A je poněkud zmanipulovaná, takže vyhraji, pokud přistane na preferované straně, a vy vyhrajete, pokud přistane na druhé straně. Můžete tedy vyhrát pouze s pravděpodobností 49,5 procenta a v tomto případě vám dám 1 $; jinak mi zaplatíte stejnou částku.

Pokud hrajete hru A proti mně mnohokrát, nevyhnutelně utrpíte mnoho ztrát, protože mi musíte platit v průměru jeden cent za hru. (Můžeme to rychle vypočítat tak, že vezmeme pravděpodobnost vaší výhry a odečteme pravděpodobnost mé výhry: 0,495 – 0,505 = –0,01.)

O podpoře vědecké žurnalistiky

Pokud se vám tento článek líbí, zvažte podporu naší oceňované žurnalistiky předplatné. Zakoupením předplatného pomáháte zajistit budoucnost působivých příběhů o objevech a nápadech, které formují náš dnešní svět.

Pak je tu druhá, složitější hra „B“, která zahrnuje roztočení dvou kol štěstí. V této hře budete moci točit jedno nebo druhé podle toho, kolik peněz aktuálně máte. Pokud je váš dostupný kapitál pro hru (na základě toho, jak jste hráli A) rovnoměrně dělitelný 3, pak roztočíte kolo štěstí, které vám dává šanci na výhru pouze 9,5 procenta. Pokud naopak váš kapitál není dělitelný 3, získáte lepší kurz: roztočíte další kolo, které vám dává 74,5procentní šanci na výhru.

Teď jsou věci zajímavé.

Dvě hry, které můžete jen prohrát

Ve hře B je sázka opět 1 dolar. V průměru ztratíte 87 centů za zatočení.

Pojďme se v tom rýpat. Mohli byste předpokládat, že jednu třetinu času roztočíte kolo, které je pro vás nevýhodné, a dvě třetiny času točíte druhé kolo. Ale to je nesprávné, protože vaše peníze nekolísají rovnoměrně. Pokud máte například 9 dolarů, roztočíte nepříznivé kolo a pravděpodobně prohrajete, takže vám zůstane pouze 8 dolarů. Pokud však hru budete hrát znovu s touto částkou, roztočíte kolo, které je pro vás výhodnější, a budete mít vyšší šanci na výhru. Takže opět skončíte s 9 dolary.

Pravděpodobnost, že máte peněžní částku dělitelnou 3, je tedy výrazně větší než jedna třetina. Pomocí složitého postupu známého jako Markovův řetězec můžete vypočítat, že vaše celková pravděpodobnost výhry ve hře B je pouze 49,565 procent – ​​a váš očekávaný zisk na kolo je záporný: 0,49565 – 0,50435 = –0,0087.

Objevuje se paradox

Pokud jste chytří, nehráli byste proti mně ani ve hře A, ani ve hře B. V obou případech musíte z dlouhodobého hlediska prohrát. Parrondo si ale uvědomil, že smíšená strategie se může vyplatit: střídáním her A a B můžete skutečně celkově vyhrát.

Pokud například hrajete vždy dvě kola hry A následovaná dvěma koly hry B, vyhrajete v průměru 1,48 centu za kolo. Nebo pokud budete po každém kole A sledovat dvě kola B, vyděláte v průměru 5,8 centů za kolo. Z dlouhodobého hlediska byste tedy viděli zisk v obou případech.

Jak Parrondo zjistil, existuje více kombinací A a B, které pro vás mají kladnou očekávanou hodnotu, než naopak. Vycházíte tedy jako vítěz, i když si náhodně vyberete, zda budete každé kolo hrát A nebo B (například tím, že necháte rozhodnout spravedlivou minci). V tomto případě je vaše průměrná výhra 1,47 centů za kolo.

Jak je to možné? Klíčem k paradoxu Parronda je, že dvě hry A a B se mohou navzájem ovlivňovat, protože hra B závisí na penězích, které aktuálně máte, a tato částka kolísá, jak hrajete hru A. A a B proto již nelze považovat za nezávislé hry. To je jádro Parrondova paradoxu. Pokud by byla hra B upravena tak, že by například hodnota kostky určovala, které kolo štěstí roztočíte, paradox by zmizel, protože obě hry by byly na sobě zcela nezávislé.

Aplikace Parrondova paradoxu

Od překvapivé publikace Parronda v roce 1996 se na toto téma objevilo mnoho článků. V roce 2017 demonstrovali dva informatici že tento paradox může vysvětlit různé životní strategie slizniček, které se mohou střídat mezi osamělým, kočovným životem a stacionární kolonií.

V některých situacích je pro tyto bytosti výhodnější shromáždit se a vytvořit kolonie místo toho, aby existovaly jako osamělí tuláci. Ale ani tato komunitní uspořádání života nemohou dlouhodobě přežít: organismy využívají své prostředí a nakonec se zdroje začnou vyčerpávat. Lpění na jedné strategii by nevyhnutelně vedlo ke smrti, ale smíšená strategie nabízí řešení: organismy se dočasně znovu stanou mobilními, zatímco se prostředí v určité oblasti regeneruje.

Výpočetní fyzik Jian-Yue Guan z Lanzhou University v Číně a její kolegové představili další aplikaci Parrondova paradoxu v článku publikovaném v Fyzický přehled E v srpnu 2025. U mnoha typů rakoviny se používají dva různé přístupy k chemoterapii. Pacienti buď dostávají maximální tolerovanou dávku ve specifických intervalech, nebo jsou trvale léčeni nízkou dávkou. První strategie má tu nevýhodu, že některé nádorové buňky si vyvinou rezistenci, a tak nereagují na medikaci. Ve druhé strategii není koncentrace léčiva vždy dostatečně vysoká, aby zcela vymýtila všechny rakovinné buňky.

Prostřednictvím počítačových simulací vědci prokázali, že přepínání mezi dvěma léčebnými přístupy v nastavených časech by mohlo vést k lepším výsledkům i bez podrobného sledování – podobně jako náhodné pořadí A a B je výhodné v příkladu loterie. Zda lze tento teoretický přístup skutečně aplikovat na medicínu rakoviny, vyžaduje další zkoumání. Guan a její tým plánují otestovat své nápady pomocí studií in vitro.

Tento článek se původně objevil v spektrum vědy a byl reprodukován se svolením.