Matematici najdou důkaz 122leté puzzle trojúhelníku

Matematici najdou důkaz 122leté puzzle trojúhelníku
Nakonec bylo vyřešeno dlouhodobé tajemství tvaru
Ilustrace polygonů řazení tvaru.
Asi před deseti lety TonnorsNyní matematik v Japonsku Advanced Institute of Science and Technology (Jaist) stál fascinován před výstavou Origamilike matematického muzea. To představovalo trojúhelníkovou dlaždici nakrájenou na čtyři kusy, které byly spojeny malými panty. S jednoduchým otokem se kousky otočily, aby transformovaly trojúhelník na čtverec.
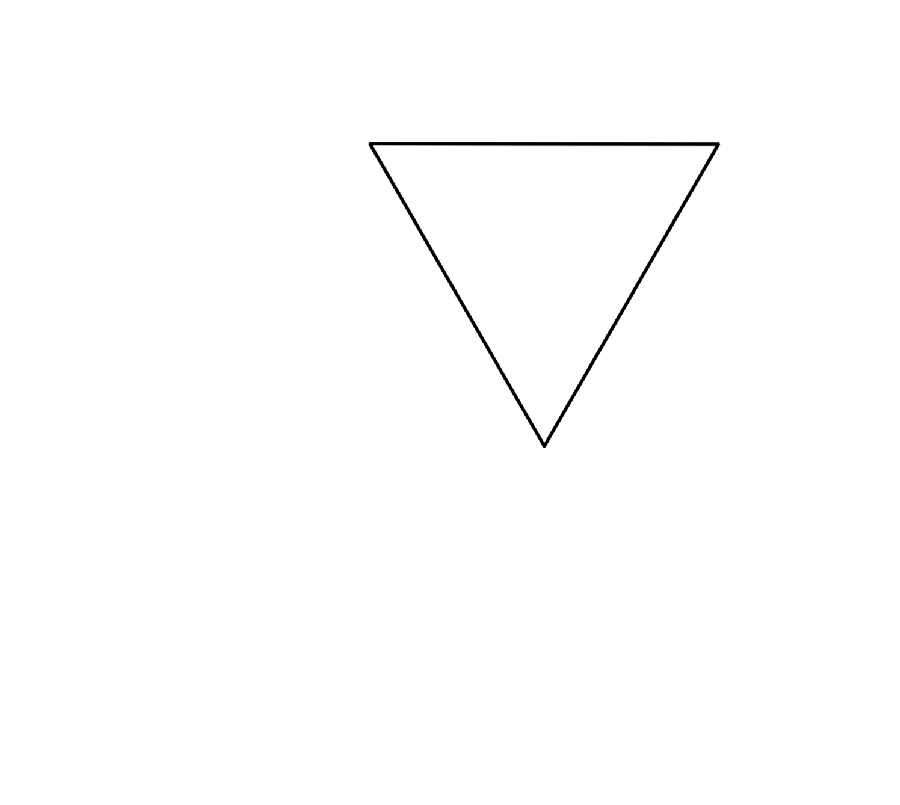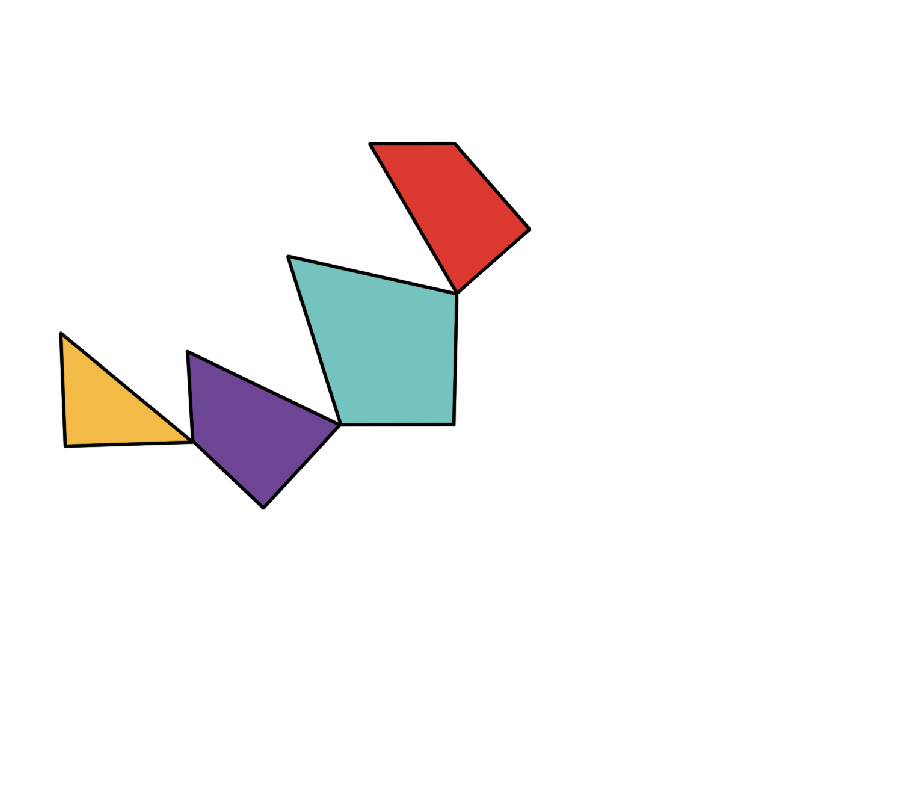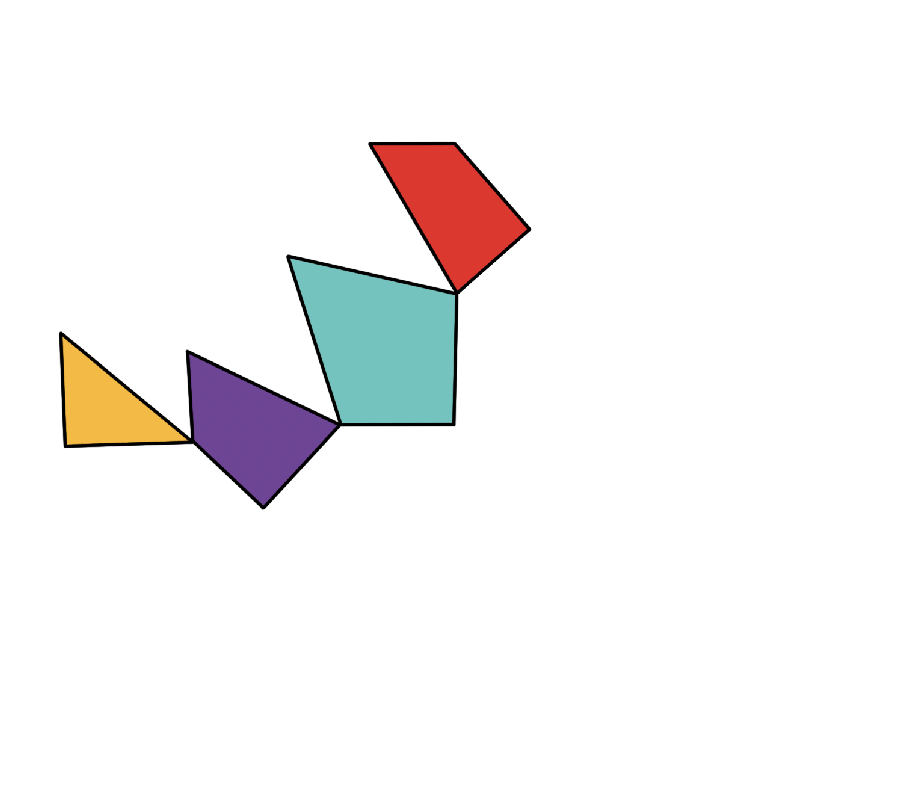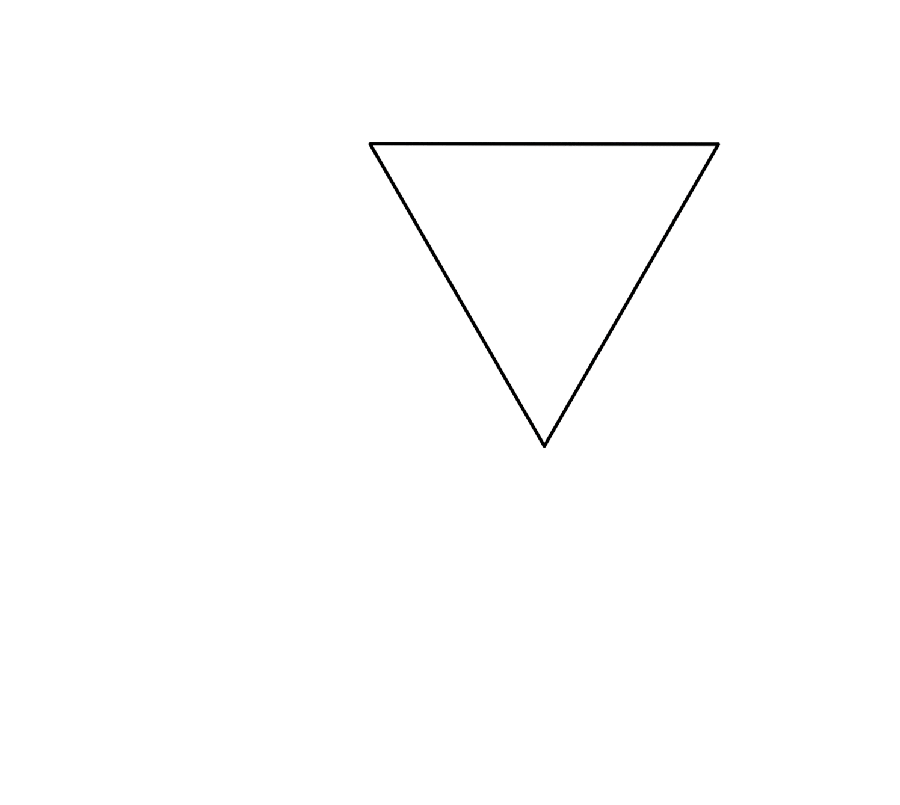
Výstava sleduje jeho původ k matematické hádance publikované v novinách z roku 1902. Henry Dudeneyanglický matematik a samouk hádanka publicista, požádal své čtenáře, aby prosadili rovnostranný trojúhelník do nejmenšího počtu kusů, které by se mohly přeskupovat na čtverec. Ve svém příštím sloupci o dva týdny později poznamenal, že „pan CW McElroy z Manchesteru“-Scarles William McElroy, úředník, který často psal Dudeneymu s puzzle roztoky-měl čtyřdílné řešení. Po dalších dvou týdnech Dudeney oznámil, že žádný z ostatních čtenářů novin toto řešení nevyužil, a od té doby záznam stál. Zůstalo to však neprokázané, zda existovalo řešení s menším počtem kusů.
O podpoře vědecké žurnalistiky
Pokud se vám tento článek líbí, zvažte podporu naší oceněné žurnalistiky předplatné. Zakoupením předplatného pomáháte zajistit budoucnost působivých příběhů o objevech a myšlenkách, které dnes formují náš svět.
Hádanka se stala známou jako „Dudeneyova disekce“ nebo „Haberdasherův problém“ a byla dokonce uvedena v Vědecký Američan‚s Červen 1958 vydání. Martin Gardner, matematik a dlouholetý publicista časopisu, psal o quandary.
(Vyzkoušet Vědecký AmeričanMatematické hádanky)
Nyní, více než 122 let poté, co bylo poprvé navrženo, Kamata a dva další matematici konečně prokázali, že řešení s menším počtem kusů je nemožné. Jejich výsledek byl vyslán na server arxiv.org v předtisku prosince 2024 s názvem “Dudeneyova pitva je optimální“
„Věřím, že mnozí, kteří oceňují matematiku, by souhlasili s tím, že čím jednodušší se objeví nevyřešený problém, tím hlubší podmanivá se stává těm, kteří milují matematiku,“ říká Kamata.
Společně s Massachusetts Institute of Technology Matematik Erik Demaine a Jaistovým matematikem Ryuhei Uehara, Kamata vyvinula nový přístup k řešení problémů s origami-složením pomocí teorie grafů. V teorii grafů je graf v podstatě sbírkou řádků nebo okrajů a vrcholů, body, kde se hrany setkávají. Hrany a vrcholy jednoho grafu lze porovnat s předměty jiného, aby prozkoumaly hlubší vztahy mezi oběma strukturami – přístup, o kterém si myslel Kamata, může pomoci vyřešit Dudeneyovu pitvu.
Jedna část problému je poměrně jednoduchá: dvoudílné řešení lze vyloučit přemýšlením o omezeních problému. Pro začátek musí mít trojúhelník a čtvercové stejné oblasti, protože kusy jsou stejné. Pro čtverec je jeho nejdelší možný řez napříč diagonálem. Trochu matematiky pero a papíru ukazuje, že bohužel délka diagonálu je příliš krátká pro okraj svého trojúhelníku ve stejné oblasti, který vylučuje dvoudílné řešení.
Dokazování, že neexistují žádná třídílná řešení, je však mnohem složitější, a to je důvod pro zpoždění století. Ačkoli se jedná o jednoduchou třídílnou hádanku, existuje nekonečný počet způsobů, jak rozřezat trojúhelník, říká Demaine. „Každý z těchto kusů by k němu mohl libovolně mnoho okrajů a souřadnice těchto škrtů začínají na libovolných bodech,“ říká. „Máte tyto nepřetržité parametry, kde je spousta a spousta nekonečnosti možných možností, díky nimž je tak nepříjemně tvrdě. Nemůžete to jen brutální silou počítačem.“
Aby se problém vyřešil, skupina kategorizovala možné disekce rovnostranného trojúhelníku na základě toho, jak se řezy protínají hrany trojúhelníku. Nejprve vědci třídili nekonečno způsoby, jak snížit trojúhelník na pět jedinečných klasifikací. Poté opakovali cvičení na čtverci a našli 38 různých klasifikací.
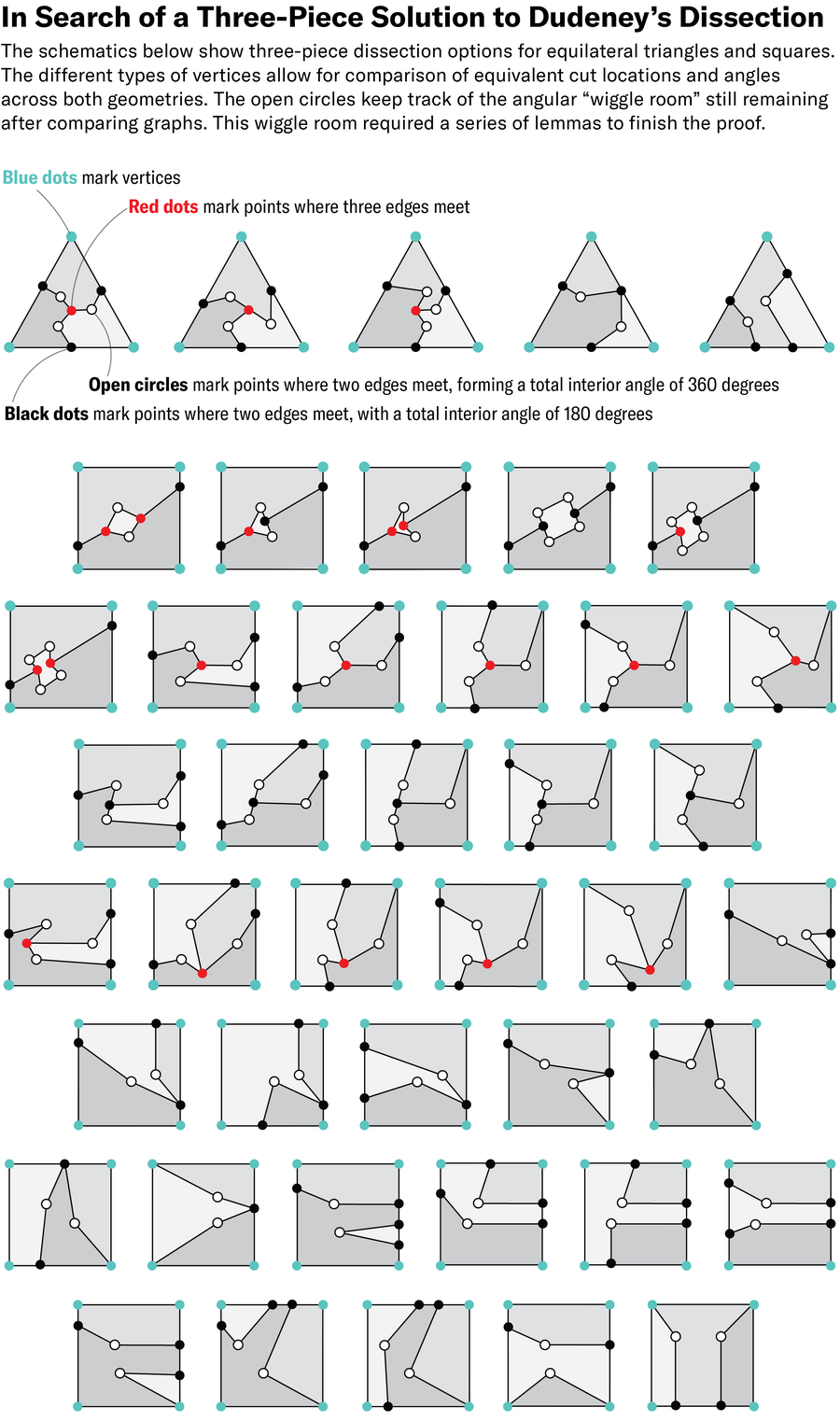
Dále se vědci pokusili porovnat trojúhelníkový graf s čtvercovým způsobem sledováním všech možných cest v každém tvaru a porovnáním výsledných sbírek délek a úhlů. Pokud by jedna z cest čtverců odpovídala cestě trojúhelníku, znamenalo by to, že vědci objevili třídílné řešení.
Tento přístup přeměnil nepřetržitý problém na diskrétní – téměř. V rámci každé klasifikace je „stále nekonečně mnoho míst, které by všechny tyto vrcholy mohly jít,“ říká Demaine. Nakonec skupina odvodila sbírku složitých lemmů nebo mezilehlých kroků v větě, která spolu s kategoriemi použila důkaz na rozpor, aby nenašla žádné odpovídající cesty.
Smith College Computer Scientist Joseph O’Rourke, který má zápasil s puzzle Po celá desetiletí a vypínání a nebyl zapojen do současné práce, myslí si, že důkaz skupiny lze pravděpodobně zjednodušit. Poznamenává, že k odstranění všech možností, „mnoho dalších vědců by se vzdalo, trvalo chaotickou sbírku vysoce specifických lemmů.“
Je důležité, že pokud autoři dokážou zjednodušit svůj důkaz, technika odpovídajících diagramů by mohla odhalit zabitím příbuzných otevřených otázek origamiliku. „Tyto problémy nám připomínají, kolik toho ještě není třeba objevit,“ říká Kamata. „Kdokoli se může stát průkopníkem v této hranici.“




