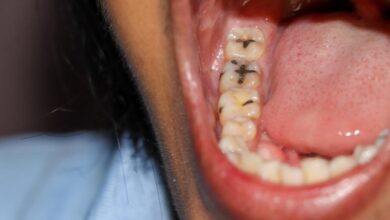
Vyzkoušejte tyto logické hádanky z mezinárodní logické olympiády
Jak jste logičtí? Vyzkoušejte své dovednosti s těmito problémy z nové mezinárodní logické olympiády
Pouze ve svém druhém roce se mezinárodní logická olympiáda již rozvíjejí, protože logika se v našem neustále se měnícím světě stává stále důležitějším
Začátkem tohoto měsíce vyšla 36 studentů středních škol z celého světa na teplé a svěží kampus na Stanfordské univerzitě. Z více než 4 000 studentů z více než 2 000 škol ve více než 90 různých zemích bylo těchto 36 lidí vybráno, aby soutěžily jako finalisté ve druhé mezinárodní logické olympiádě (ILO).
Soutěž zahrnovala tři kola testů, které vyvrcholily posledním ve Stanfordu. Existují týmy dvou až čtyř se zapojily do bitvy o rozumu, řešení Logické hádanky a soutěžit Matematické hry Na pozadí úpatí Palo Alto v Kalifornii. V letošním roce byli studenti 11. ročníku Luke, Zixuan Yin, Kingston Zhang a Max Yang, kteří se během recenze neinformálně dabovali „Team Goblin Tribe“ po přezkoumání. Klíčem k jejich úspěchu, tvrdí, byla spousta praxe a týmové práce. „Myslím, že část důvodu, proč jsme v tom byli schopni tak dobře, bylo proto, že znám své spoluhráče opravdu dobře a my jsme přátelé už mnoho let,“ říká Song.
ILO byl zahájen počítačovým vědcem a logikem Stanfordu Michael Genesereth ve spolupráci mezi univerzitou a vzdělávacími neziskovými luminami. „Logiku používáme téměř ve všem, co děláme,“ říká Genesereth. Lékaři používají logiku k diagnostice pacientů, právníci používají logické argumenty v soudní síni a logika je nezbytnější než kdy jindy k vyhodnocení rychle se měnícího světa kolem nás poznamenává. „To všechno nemá co do činění s matematikou a vzorci a algebrou,“ dodává Geneseth.
O podpoře vědecké žurnalistiky
Pokud se vám tento článek líbí, zvažte podporu naší oceněné žurnalistiky předplatné. Zakoupením předplatného pomáháte zajistit budoucnost působivých příběhů o objevech a myšlenkách, které dnes formují náš svět.
Většina letošních vítězů má zájem o informatiku, spolu s environmentální vědou, aplikoval matematiku a elektrotechniku, ale Zhang říká, že ani matematika ani počítačová věda není jeho „silným oblekem“ a že plánuje jít do politologie. „Mnoho problémů vyžaduje velmi rozsáhlé myšlení a kreativní řešení a myslím si, že mi to určitě pomůže, pokud v budoucnu půjdu do politiky,“ vysvětluje.
Zvláštní aspekt Olympiády je její spolupráce, ve které týmy spolupracují na řešení problémů, říká Yin. Obzvláště byl hrdý na to, jak on a jeho spoluhráči spolupracovali na hádanky s názvem Nations (níže). Poté, co odůvodnil, že řešení, které nabízí jeden z členů jeho skupiny, musí být špatné a přišlo s alternativním řešením, které se ukázalo jako správné, že spoluhráč „právě mi říkal, jak štěstí mě má mít ve svém týmu,“ říká Yin. „Mít tyto úžasné lidi, aby pracovali na logice – je to něco, co spojuje skupinu našich přátel dohromady.“
Zde je několik kurátorských hádanek z konkurence, na které si můžete vyzkoušet svou vlastní skupinu přátel. Některé z hádanek byly upraveny tak, aby lépe odpovídaly formátu tohoto článku.
Přátelé
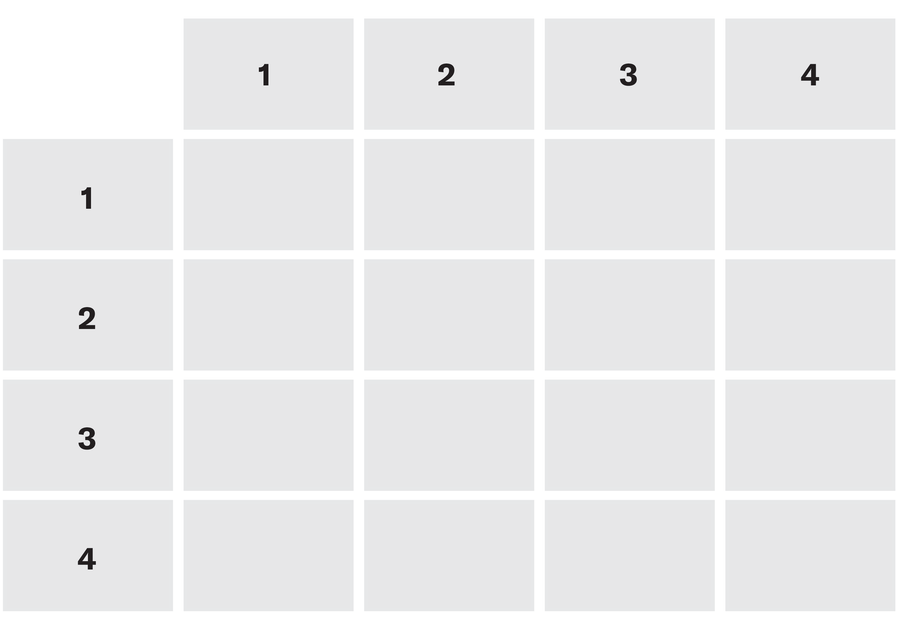
Čtyři studenti, očíslovaní 1, 2, 3 a 4, mezi sebou hlasují, aby určili, kdo by měl vést revizi. Každý student je povinen hlasovat „ano“ nebo „ne“ pro každou osobu ve skupině, včetně sebe. Následuje skutečná prohlášení o jejich hlasovacích lístcích:

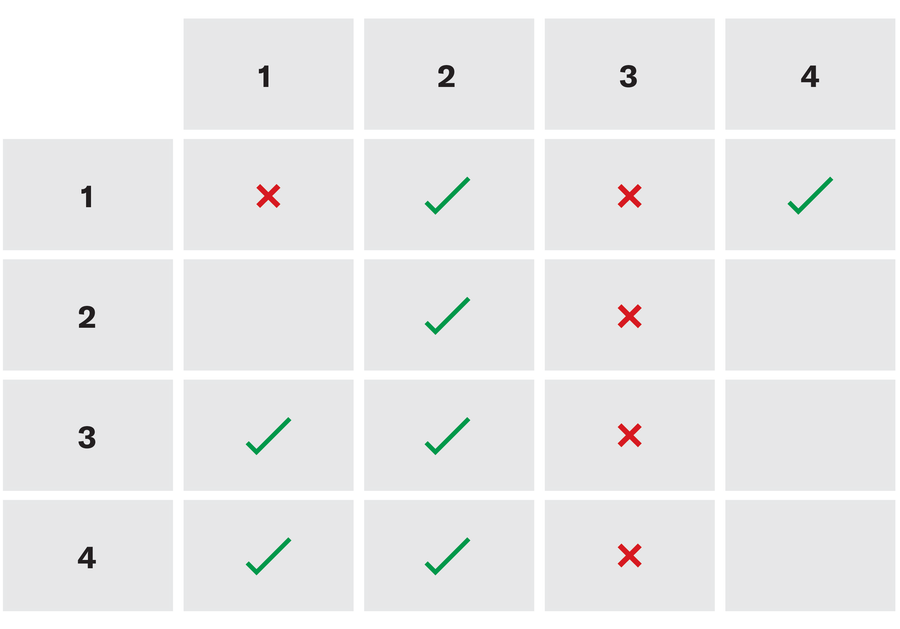
Ve výše uvedené tabulce jsou prohlášení původního problému ILO v jazyce matematické logiky vpravo. Naše překlady těchto prohlášení jsou vlevo.
Zjistěte, pokud je to možné z těchto prohlášení, kteří a nehlasovali, pro koho. Vyplňte to v následující mřížce šekem na hlasování ANO, „X“ pro bez hlasování a prázdné, pokud to nemůžete vědět s jistotou. Každý řádek představuje hlasování čísla uvedeného vlevo.
Poznámka: Pokud máme prohlášení A To není pravda, zvažujeme jakoukoli větu formuláře „Pokud A, pak B„Abych to byla pravda. Například„ Pokud je obloha zelená, pak je pravda, bez ohledu na to, co se děje v prázdné, protože předpoklad je nepravdivý. Tuto skutečnost budete potřebovat k vyřešení hádanky.
Kvíz
1. Jaká je odpověď na otázku 2?
A. b
B. a
C. d
D. c
2. jaká je odpověď na otázku 3?
A. c
B. d
C. b
D. a
3. jaká je odpověď na otázku 4?
A. d
B. a
C. c
D. b
4. Jaká je odpověď na otázku 1?
A. d
B. c
C. a
D. b
Bezpečné praskání
Kombinovaný trezor je otevřen řadou čtyř přepínačů, které lze převrátit na (1) nebo vypnuto (0). Trezor je rozbitý, takže abyste jej mohli otevřít, musíte pouze získat pozici dvou konkrétních přepínačů – ale neexistuje způsob, jak vědět, které přepínače jsou ty, na kterých záleží. Najděte nejmenší sadu kombinací, které se můžete pokusit zaručit, že jeden z nich otevře trezor.
Národy
Existují dva typy národů: silné a slabé. Mohou být napadeny pouze slabé národy a mohou napadnout pouze silné národy. Pokud silný národ napadne slabý národ, bude připojit slabý národ, ale po určitou dobu se stane slabým, a tedy invazibilním. Pouze jeden silný národ může napadnout slabý národ najednou. Pokud se více národů rozhodne napadnout stejný slabý národ, je náhodně vybráno, aby bylo možné napadnout. Každý národ chce být co nejvíce velký, ale ne na úkor, který by byl připojen sám. Předpokládejme, že všechny národy jsou zcela racionální. Existuje pět silných národů a jeden slabý národ. Bude napaden slabý národ?
Tip: Zkuste nejprve začít s jedním silným národem a jedním slabým národem a pak se odtamtud vybudujte. Chcete -li problém vyřešit, zkuste zjistit, jak složité případy lze snížit na jednodušší – metodu formálně známou jako „matematická indukce“.
Puzzle Sudoku
Tato hádanka byl také zahrnut do ILO. Konkurenti to museli vyřešit pod časovým limitem pomocí pouze tužky a papíru.
Přátelé
Kvíz
1. d
2. c
3. b
4. a
Bezpečné praskání
Chcete -li zaručit, že můžete prasknout trezor, budete muset mít všechny možné sady pozic pro každou zastoupenou dvojici přepínačů. Tímto způsobem, bez ohledu na to, které dva přepínače jsou ty, na kterých záleží nebo které pozice otevírají trezor, jeden z kódů to praskne. Minimální počet potřebných kombinací je pět. Zde je jedno možné řešení: 1000, 0100, 0010, 0001, 1111.
Národy
Zde je jeden způsob, jak si to promyslet. Předpokládejme, že máme jeden silný národ a jeden slabý národ. Silný národ bude přirozeně chtít napadnout slabý národ, protože neexistuje žádný jiný národ, který by napadl silný po tom, co tak učiní. A co dva silné národy a jeden slabý národ? Pokud by jeden ze silných národů připojil slabý národ, dočasně by se stal slabým a napadl by druhý, takže ani jeden z nich by nechtěl napadnout na první místo, protože věděl, že budou napadeni hned zpět. Nyní zvažte tři silné národy a jeden slabý národ: Pokud si silný národ napadne, zůstanou se dvěma silnými národy a jedním slabým národem, situací, ve které jsme právě určili, že nikdo nenapadne – takže všechny tři silné národy by v tomto případě chtěly napadnout. S využitím stejné logiky, pokud existují čtyři silné národy a jeden napadne, scénář se sníží na případ tří silných národů, kdy by všichni chtěli napadnout, takže žádný ze čtyř národů by na prvním místě riskoval. Nakonec nás to vede k pěti silným národům a jednomu slabému národu, scénáři, ve kterém by všechny silné národy chtěly napadnout, protože jakmile budou čtyři silné národy a jeden, který se stal slabým při připojení, nikdo nebude napadnout.