Jak dospívající matematika Hannah Cairo vyvrátila hlavní dohad v harmonické analýze

Když bylo Hannah Cairo 17 let, vyvrátila dohad Mizohata-Takeuchi, což je dlouhodobý odhad v oblasti harmonické analýzy o tom, jak se vlny chovají na zakřivených površích. Domněnka byla uvedena v 80. letech a matematici se to od té doby snažili prokázat. Pokud by se domněnka Mizohata-Takeuchi ukázala jako pravdivá, osvětlilo by to mnoho dalších významných otázek v terénu. Ale poté, co zasáhl zeď za snahou o to, aby se o to dokázal, se Kahiorovi podařilo přijít s protikladem: okolnost, kde se vlny nechovají, jak předpovídá dohad. Domněnka proto nemůže být pravdivá.
Káhira se na problém spojila poté, co jí byla přidělena jednodušší verze domněnky, která by dokázala jako domácí úkol pro třídu, kterou absolvovala na Kalifornské univerzitě v Berkeley. „Chvíli mi trvalo, než jsem přesvědčil (instruktor kurzu) Ruixiang Zhang, že můj návrh byl ve skutečnosti správný,“ říká. Nyní, pod poradenstvím Zhangu, má papír na předtiskovém serveru arxiv.org a byla vyzvána, aby představila své výsledky na mezinárodní konferenci o harmonické analýze a částečných diferenciálních rovnicích ve Španělsku Elshing.
O podpoře vědecké žurnalistiky
Pokud se vám tento článek líbí, zvažte podporu naší oceněné žurnalistiky předplatné. Zakoupením předplatného pomáháte zajistit budoucnost působivých příběhů o objevech a myšlenkách, které dnes formují náš svět.
Cairo říká, že miluje mluvit o svém výzkumu a poskytovat prezentace s barevnými a popisnými snímky (viz příklady níže). Když se zeptal, co studuje, Káhira zkrátka říká: „Body, linky a vlny.“
Narodila se a vyrůstala na Bahamách, Káhira se přestěhovala do Kalifornie ve věku 16 let, kde začala chodit v UC Berkeley. Nyní, ve věku 18 let, je na Ph.D. Program na University of Maryland, aby pokračoval ve svém výzkumu v teorii Fourierovy omezení. Káhira čelila mnoha obtížím na své cestě, ale ona našla pohodlí a sounáležitost v oblasti matematiky a samotné práce.
Vědecký Američan Mluvil s Káhirou o způsobu, jakým je harmonická analýza jako odhození kamenů do nehybného rybníka, její transgender identity a důvody, proč miluje matematiku.
(Následuje upravený přepis rozhovoru.)
Kromě „bodů, řádků a vln“, jak byste vysvětlil své studijní pole, harmonická analýza?
Představte si, že jste u rybníka a je to velmi stále rybník a do něj vložíte kámen. Vidíte, jak se tyto kruhové vlny šíří.
Pokud v rybníku upustíte dva kameny, můžete si všimnout, že tento vzor nazývá vzorec interference: místo toho, aby vypadali jako kruhy, se překrývají. Získáte vysoké body, nízké body. A dostanete tyto zajímavé tvary (kde se protínají). Co kdybyste měli použít celou spoustu vlnky – pak co byste dostali? V harmonické analýze můžete skutečně prokázat, že pokud své kameny upustíte na správném místě v rybníku, můžete získat jakýkoli tvar, který chcete.

Snímek z prezentace Hannah Cairo na dohad Mizohata-Takeuchi
Moje specialita je známá jako Fourierova restrikční teorie, což je subdisciplína harmonické analýzy, ve které pracuji, kde se ptáme, jaké objekty můžeme postavit, pokud máme povoleno používat pouze určité druhy vln. Co když máme dovoleno pouze upustit kameny v určitých částech rybníka? Nebudete moci získat jen žádný objekt. Ve skutečnosti budete moci získat relativně malou rodinu předmětů. To, co říká domněnka Mizohata-tak-takeuchi, je, že tvar objektů, které dostaneme, je soustředěn podél linií.
Co to znamená být „soustředěno podél linií“?
Jedním ze způsobů, jak myslet na tvar objektů, je zeptat se: Co je zakřivení? Existuje několik různých způsobů, jak jej můžete definovat. Jedním možným způsobem je vzít tenký, dlouhý obdélník a zeptat se, kolik z vašeho kruhu může ležet v tomto tenkém obdélníku. To, co zjistíte, je, že to není moc z toho, protože se ohýbá pryč, že? Na druhou stranu, pokud vezmete něco plochého jako okraj čtverce, můžete získat celou stranu tohoto čtverce jen na jedné tenké trubici. To znamená, že čtverec není tak „zakřivený“ jako kruh.
Pro domněnku Mizohata-Takeuchi říkáme, že tento předmět stavíme z těchto vln. A chceme říci, že na tvarech, které neobsahují příliš mnoho řádků nebo tenkých obdélníků, nebude moc lhát.
Jak se vám tedy podařilo vyvrátit tuto domněnku?
Podíval jsem se na tyto tvary a jedna věc, kterou jsem si uvědomil, je, že specifický druh vln, které se používají, jsou koncentrovány podél silných obdélníků. To je vlastně něco, co je dobře známé. Takže se nakonec podíváte na tyto vlny, které se soustředí na obdélníky: berete tyto vlny a navzájem se protínají a tyto určité tvary vytvářejí, ale zde (místo kruhových vln) používáme vlny obdélníků. Takže pak máme všechny tyto obdélníkové vlny, které se navzájem setkávají. Uvědomil jsem si, že tvar místa, kde se setkávají, není zcela na pravém úhlu, aby souhlasil se směrem, do kterého tyto obdélníky směřují. A tak mě to vedlo k poněkud komplikované konstrukci pomocí fraktálů k uspořádání těchto obdélníků.
Původní fraktální konstrukce se však ve vašem papíru ve skutečnosti neobjeví. Jaký byl váš poslední protiklady?
Zjistil jsem to, že pokud tyto vlny uspořádáte tím, že vezmete vysokorozměrnou hypercube a promítáte ji do menšího dimenzionálního prostoru a pak vezmete pouze ty vlny, které leží ve vašem regionu, pak takto můžete určit, kam je můžete dát (prolomit dohad).
Co vás poprvé zajímalo o matematiku?
Vždycky mě zajímalo matematiku. Myslím, že pro mě je matematika umění. V mém dětství jsem byl poněkud osamělý. Matematika tam byla jako přítel téměř. Myslím, že umění nemusí být nutně přítelem ve všech ohledech, kterým může být přítel, ale myslím, že umění je jako přítel. A tak, tak dlouho, jak si pamatuji, jsem vždy miloval matematiku.
Řekněte mi více o tom, jak byla pro vás matematika přítelem. Myslím, že mnoho lidí nemyslí na matematiku jako na velmi přátelskou.
Je tu analogie, kterou rád dělám, což je k jiné formě umění: malby. A myslím si, že kdyby někdo měl třídu na barvu, můžete si zapamatovat data a časy, kdy byly vyvinuty různé formy barvy – a možná i ty barvy byly použity, kterými malíři. A pak můžete zjistit, jaké procesy můžete použít k určení, jaký typ barvy to je. Představuji si, že je to užitečné v historii umění, ale to není umění …. Neměl bych to říkat. Možná existuje umění učit se o barvě. Nebudu tvrdit, že to není proto, že nebudu studovat barvu. Ale myslím, že matematika je trochu taková – ve škole se lidé učí (matematická verze) barvy; Neučí se o malbě.
Matematika je pro mě uklidňující, protože je to způsob, jak prozkoumat – prozkoumat myšlenky a přemýšlet o nich a vybudovat více nápadů z jiných nápadů. Co je na tom uklidňující, je to, že je v některých ohledech nezávislý na světě. Pokud mám smutný den, šťastný den, pokud se přesunu do Marylandu (právě jsem se přestěhoval do Marylandu), matematika je stále tam a je to stále totéž. Je to také něco, co mi může obsadit mysl.
Zmínil jsi mi, že jsi transgender. Jak to ovlivnilo vaši cestu?
Myslím, že je to pravděpodobně důležitější na mé cestě jako člověka než jako matematik. Být trans přiměl mě vidět věci o světě, které bych jinak neviděl. Přinutilo mě to vidět svět jinak a přimělo mě, abych viděl lidi jinak a přiměl mě, abych se viděl jinak.
Naštěstí si v matematické komunitě myslím, že většina matematiků je v pořádku s trans -lidmi. Myslím, že to bylo významnější (v mém každodenním) než nyní. V dnešní době to opravdu nezmění.
Proč jste se rozhodli jít na rekord nyní jako trans?
Transdibilita je důležitá. Lidé mají představy o tom, kdo jsou trans lidé, a myslím si, že je nejlepší to rozšířit. Možná také doufám, že lidé, kteří si myslí, že trans -lidé jsou „méně“ než lidé Cisgender, by se o to mohli ptát.
Druhou věcí je, že je dobré, aby trans lidé věděli, že nejsou sami. Myslím, že část toho, co pomáhá trans lidem, si uvědomují, že jsou trans, je vědět, že existuje více možností, kým můžete být jako trans -osoba. To je pro mě důležité.
Děkuji moc za sdílení. Kde je vaše oblíbené místo k matematice?
Pokud se snažím být produktivní při psaní něčeho, pak rád jsem u svého stolu a rád poslouchám Bacha. Pokud se jen pokouším přemýšlet o nápadech, pak moje oblíbené místo, kde to udělám, je někde, kde nemusím věnovat pozornost moc jiného. Mohl bych jen někde posadit a přemýšlet o věcech, nebo bych mohl jít na procházku venku.
Také rád mluvím s ostatními lidmi o matematice, což je další druh matematiky. Opravdu rád předkládám matematiku. Mám tyto ručně psané snímky se všemi těmito barvami a výkresy. Naštěstí v harmonické analýze mohu představit takovou prezentaci a pak jsou všichni tak šťastní a říkají mi, že moje snímky jsou roztomilé.
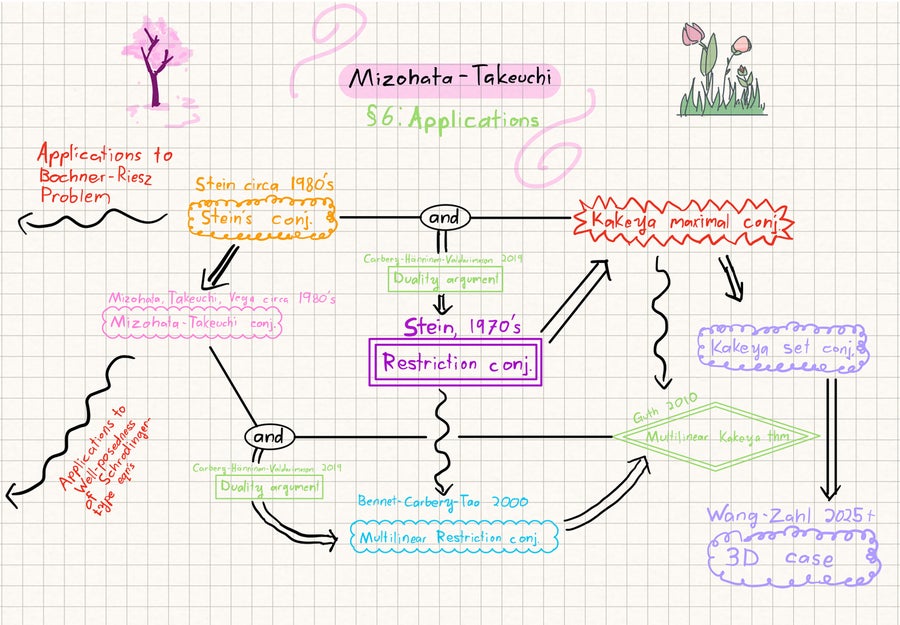
Poslední snímek z Káhiry prezentace na dohad mizohata-takeuchi
Co bude dál pro váš výzkum?
Pracuji na výzkumném projektu se svým poradcem na Mizohata-Takeuchi a přilehlých věcech a asi jako je jiná věc: místní Mizohata-takeuchi dohad.
Proces učení se více o tomto druhu matematiky je docela vzrušující – nejen pro mě se dozví více o tom, co je tam, ale pro matematickou komunitu jako celek se snaží lépe porozumět těmto druhů věcí. (To je) něco, na co jsem nadšený.




